Desenhe o diagrama de corpo livre e derive a equação de movimento pela segunda lei de movimento de Newton para cada um dos sistemas mostrados nas figuras 2.74 e 2.75.
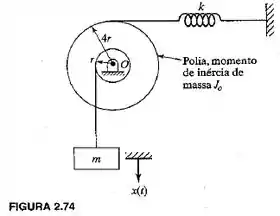
Fonte: Rao Vibrações Mecânicas – 4ª ed
Passo 1
Fala aí meus queridos!
Bora dar continuidade à temida Vibrações haha!
O problema em questão nos pede o diagrama de corpo livre que a gente tanto conhece e a equação do movimento pela segunda Lei de Newton.
Vamos lá!
Passo 2
Lembrando que a segunda Lei de Newton diz que o somatório das forças do sistema em movimento é igual ao produto da massa pela aceleração do sistema.
Assim, para o bloco m:
E para a polia:
As forças são mostradas no diagrama do corpo livre:
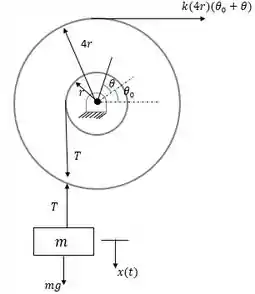
Passo 3
E é a deflexão angular da polia sobre o peso mg:
Devemos descobrir essas equações afim de substituirmos a tração T no sisteminha de equações.
Assim, substituindo as equações 1 e 3 em 2, nós temos:
Por fim, utilizando e consequentemente , temos:
Resposta
Portanto: