Determine a abscissa do centroide do trapézio da ilustração, em função de .
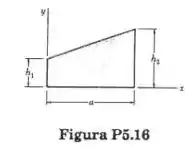
Passo 1
Boraaa galerinha, aniimaaa, vamos resolver mais um!!
Só bora então!!
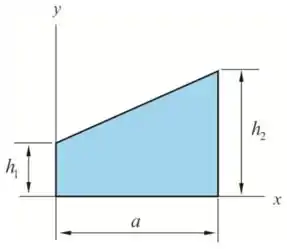
Passo 2
A área sombreada é obtida pelas seguintes áreas
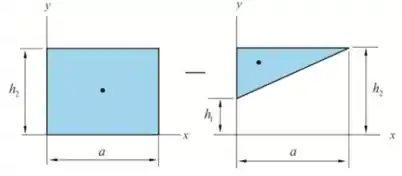
Passo 3
Os primeiros momentos das áreas componentes em relação aos eixos de coordenadas serão calculados e inseridos na tabela, como mostra a seguir:

Passo 4
A área total do trapézio
O primeiro momento da área sombreada em relação ao eixo y é de
Passo 5
A coordenada x do centroide da área sombreada é de
Portanto, a coordenada x do centroide da área sombreada é
Resposta
Portanto, a coordenada x do centroide da área sombreada é