Enunciado
Mecânica e Resistência dos Materiais - Beer - Estática- Ed: 9º - Capítulo 9.Problemas - Ex. 1
1. Determine por integração direta o momento de inércia da superfície sombreada em relação ao eixo .
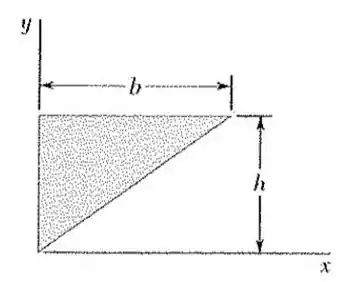
Passo 1
Bom! Primeiramente, a partir da imagem da superfície vamos fazer um esboço do elemento diferencial que servirá de base para nosso cálculo:
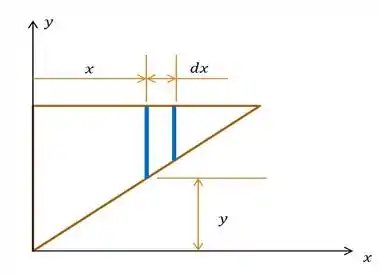
A partir desse esboço podemos estabelecer a seguinte relação proporcional, dada as dimensões da superfície que nos são fornecidas no enunciado:
Passo 2
Agora, vamos lembrar que a expressão do momento de inércia em relação a , é dada por:
A imagem não ajuda muito! Você provavelmente deve estar pensando como raios vamos obter a área daquele elemento diferencial ali; mas saiba que aquilo era pra ser um retângulo. Sendo assim, se considerarmos que o triângulo é formado por uma série de pequenos retângulos infinitesimais, a área é facilmente dada por:
Só que:
O que nos leva à:
Passo 3
Substituindo em seguida, o na expressão do momento de inércia:
Pronto! Só falta integrar essa expressão! O limite de integração é a principal úvida que pode surgir. Só que como estamos trabalhando com um diferencial em , fica fácil perceber que nosso limite vai de até :