Determine as reações de apoio da s grelhas esquematizadas na próxima figura:
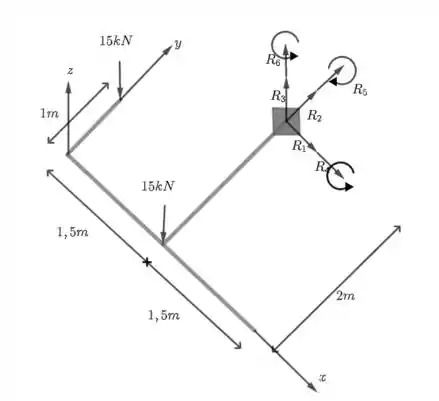
Passo 1
Fala, galerinha! Tudo beleza? Nessa questão, temos primeiramente que determinar as forças atuando na grelha e as reações de apoio. No caso de um engaste tridimensional, como na figura, temos seis reações de apoio, sendo três de força e três de momento, como mostrado na figura. Vamos usar o início do engaste como ponto de referência para as equações de equilíbrio dos momentos. Sendo assim, temos
- Uma força de atuando a uma distância de na direção e na direção em relação ao engaste tridimensional. Como essa força atua na direção , ela terá momentos somente na direção e .
- Uma força uniformemente distribuída de ao longo de . Essa força é equivalente a uma força de atuando no meio da barra ao longo da direção (veja a figura) e está a uma distância na direção .
Passo 2
Prontinho, agora que todas as forças estão identificadas, podemos utilizar as equações de equilíbrio (lembrando que os momentos no sentido anti-horário tem sinal positivo) e obter as reações:
O sinal negativo em indica que, nesse caso, o momento é no sentido horário.