Enunciado
Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 2.8 - Ex. 4v
Determine as reações de apoio dos pórticos planos esquematizados na próxima figura.
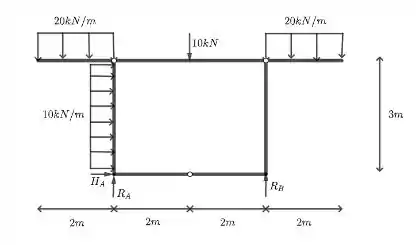
Passo 1
Temos muitas forças atuando nesse pórtico, então vamos separá-las em forças horizontais e verticais para facilitar a identificação das forças. Vamos tomar o ponto A para calcular os momentos das forças, então todas as distâncias serão tomadas em relação a esse ponto.
Forças horizontais:
Temos uma reação horizontal no ponto A e uma força uniformemente distribuída de . A força uniformemente distribuída é equivalente a uma força de aplicada no ponto , que é justamente a distância vertical até o ponto A.
Forças verticais:
Temos as reações verticais e , a força de aplicada a de A e forças uniformemente distribuídas de aplicadas entre e e entre e . A primeira delas equivalente a uma força de módulo aplicada em . Essa é exatamente a distância horizontal até o ponto A. De forma similar, a segunda força equivale a ter aplicado em , ou seja, a uma distância horizontal de de A.
Passo 2
Antes de prosseguir, é importante perceber que a força vertical de aplicada a de A e a força de reação vertical tendem a “girar” o pórtico no sentido anti-horário e, portanto, contribuirão com sinal positivo na equação de equilíbrio dos momentos. A força vertical de aplicada a de A, a força vertical de e a força horizontal de , por outro lado, tendem a “girar” o pórtico no sentido horário, ou seja, sua contribuição para a equação de equilíbrio dos momentos será negativa. Agora, podemos utilizar as equações de equilíbrio.
O sinal negativo indica que aponta no sentido negativo de .