Determine as três primeiras frequências naturais de uma viga uniforme fixa-fixa.
Passo 1
Fala galera, tranquiloo??
Vem comigo, que no caminho eu explico..
Vamos escrever a equação governante no caso de vibração transversal da seguinte maneira:
Onde :
Aqui, é densidade da viga, é o módulo de Young da viga, é a área da seção transversal da viga e é o momento de inércia da viga.
Suponha que a vida seja dividida em (n-1) parte iguais usando pontos.
Passo 2
Escreva a quarta derivada de acordo com o método de diferença
![]()
Onde
Aonde representa o deslocamento no nó é igual a .
Passo 3
Substituindo a expressão por na equação (1).
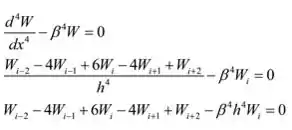
Deixei
Portanto,
Passo 4
Deixa a viga ser dividida em quatro partes de comprimento cada . Deixe haver 2 nós fictícios 0 a 6 além dos suportes fixos. Nesse caso,
Use a equação (2) para escrever as equações de diferença finita nos pontos de malha 2, 3 e 4. Da seguinte forma:
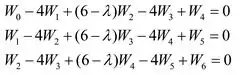
Passo 5
Neste caso, as condições de limite são:
Aplicando essas condições de contorno nas equações de diferença finita para obter as seguintes expressões:
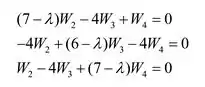
Representam as equações de diferença finita na forma de matriz da seguinte forma:
Passo 6
A equação (3) representa um problema de autovalor. Portanto, o determinante da matriz do coeficiente de deslocamento é zero. Obtenha a solução partindo da seguinte expressão:
Resolvendo essa matriz, iremos obter 3 raízes para .
Usando a seguinte expressão para determinar as frequências naturais de um feixe fixo-fixo uniforme

Passo 7
Vamos substituir 1,255 por na expressão do passo anterior para podemos obter a primeira frequência natural
Vamos substituir 6 por na expressão do passo anterior para podemos obter a primeira frequência natural
Resposta
Vide a explicação.