Determine uma única constante de amortecimento equivalente para os seguintes casos.
- Quando três amortecedores estão em paralelo.
- Quando três amortecedores estão em série
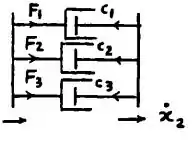
- Quando três amortecedores estão conectados a uma barra rígida (Figura 1.81) e o amortecedor equivalente está no ponto c1.
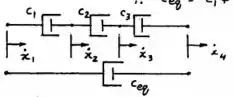
- Quando três amortecedores torcionais estão localizados a eixos engrenados (Figura 1.82) e o amortecedor equivalente está no ponto .
Sugestão: A energia dissipada por um amortecedor viscoso em um ciclo durante movimento harmônico circular é dada por onde é a constante de amortecimento, é a frequência e é a amplitude de oscilação.
Passo 1
Saalve, tudo certo? Bora pra questão sem enrolar! Aqui o jogo vai ser rápido, o processo vai ser simples mas não vamos desconsiderar porque essa questão vai nos ensinar bastante sobre o que rola quando envolve um sistema de massa mola dentro de energias potenciais e cinéticas! Vai ser interessante... vem comigo!
No item a), temos:
Passo 2
Para o item b), temos:
Passo 3
c)Equalizando as energias dissipadas em um ciclo, temos:
Passo 4
Equalizando as energias dissipadas em um ciclo,
Resposta
a)
b)
c)
d)