Um dêuteron (núcleo do átomo de deutério consistindo de um próton e um nêutron) com velocidade de colide elasticamente com um nêutron em repouso. Utilize a aproximação de que o dêuteron tem duas vezes a massa do nêutron. (a) Se o dêuteron for espalhado através de um ângulo em LAB, quais serão as velocidades finais do dêuteron e do nêutron? (b) Qual é o ângulo de espalhamento em LAB do nêutron? (c) Qual é o ângulo máximo de espalhamento possível do dêuteron?

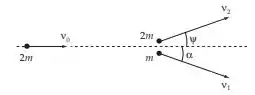
Aqui temos a imagem para ver melhor o que está acontecendo.

Primeiro vamos usar a conservação da energia cinética.

Simplificando a massa de todos os lados e o onde podemos

Agora pela conservação do momento temos

Simplificando o temos

Elevando dos dois lados ao quadrado, temos

Então temos as equações

Duas equações e três incógnitas. Pra resolver, vamos colocar e em função de que temos o valor.

O mais fácil de isolar nas duas equações é o . Então vamos isolar ele nas duas equações e igualar as duas equações que obtemos e assim vamos achar uma equação do segundo grau que relaciona e . Resolvendo essa equação, achamos a equação para

Substituindo em qualquer uma das equações, temos o valor de em relação a , que dá

Por fim, substituímos os valores que foram dados de e . Fazendo as contas, temos

Para o ângulo, usamos a lei dos senos.

Isolando temos

Substituindo os valores, vamos achar dois valores

Por fim, para a última letra temos

Substituindo o valor de vamos ter

Substituindo os valores, temos que

Assim,

E, portanto, o valor máximo de .