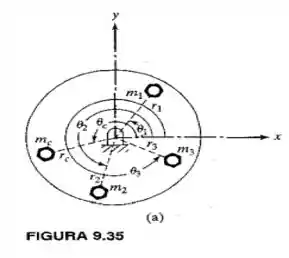
3. Dois discos idênticos estão conectados por quatro parafusos de tamanhos diferentes e montados em um eixo, como mostra a Figura 9.35. As massas e as localizações de três parafusos são as seguintes: , e ; , e e , , . Determine a massa e a localização do quarto parafuso , que resulta no balanceamento estático dos discos.
Passo 1
E aí, galerinha!
Simbora lá, meus queridos!
Bom! Baseado na figura ...
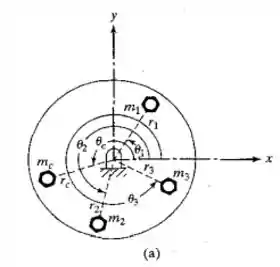
Temos que...
Passo 2
Aplicando o somatório das forças em :
E depois, aplicando o somatório das forças em :
Somando o quadrado dessas duas expressões, podemos achar a massa...
E também, podemos achar a localização...