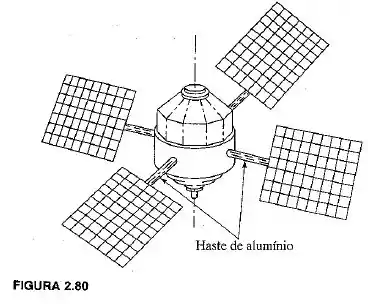
A Figura 2.80 mostra uma nave espacial com quatro painéis solares. Cada painel tem as dimensões , densidade de peso de e está ligado ao corpo da nave espacial por bastes de alumínio de de comprimento e de diâmetro. Considerando que o corpo da espaço-nave é muito grande (rígido), determine a frequência natural de vibração de cada painel em relação ao eixo da haste conectora de alumínio.
Passo 1
A massa do painel é dada por:
O momento de inércia de massa é dado por:
Passo 2
O momento polar de inercia da haste é dado por:
A rigidez torcional é dada por:
A frequência natural de vibração será: