Um fio é colocado em movimento sendo atingido em um ponto a partir de uma extremidade por um martelo triangular. A velocidade inicial é maior em e diminui linearmente a zero em e. A região inicialmente não está perturbada. Determine o movimento subsequente do fio. Por que a quarta, a oitava e as harmônicas relacionadas não estão presentes? Quantos decibéis abaixo do fundamental estão a segunda e a terceira harmônicas
Passo 1
Faaaaaala, galera... Tranquileba??
Dita as condições iniciais:
A diagrama da velocidade t=0 é:
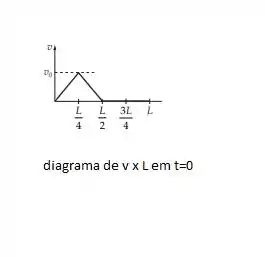
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
E temos as equações em 13.8 a e b:
Logo e
Atente que para zeramos essa equação, sabendo que com , basta fazermos , isto porque a corda está presa em e nenhuma das harmônicas nesse ponto podem ser excitadas.
Passo 3
Para temos:
E então:
Destas amplitudes podemos achar quantos decibéis abaixo do fundamental estão nos harmônicos:
Para a segunda harmônica:
Para a terceira harmônica:
Resposta
A equação de movimento é:
Não há harmônicas em na corda, ou seja, não há harmônico na quarta e oitava harmônicas, demonstração está no passo-a-passo.
E ainda, os decebeis:
Para a segunda harmônica:
Para a terceira harmônica: