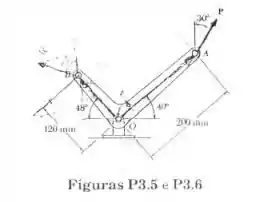
Uma força P de 300 N é aplicada ao ponto A da figura (a) Calcule o momento de P em relação a O utilizando as componentes horizontal e vertical da força (b) Como resultado parte (a), determine a distância de O à linha de ação de P.
Passo 1
Falaiii meus xuxu’s, ceis tão bonzinho??
Espero que sim hein, bora lá pra mais uma?
Encostaaaa
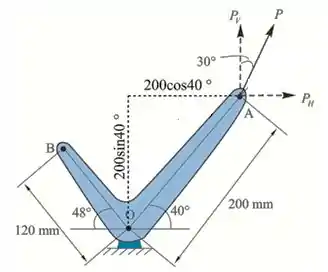
- Vamos iniciar desenhando o nosso diagrama da manivela indicando as componentes horizontal e vertical da força aplicada e as distancias entre os vários pontos
- Supondo que a força P, tenha uma distância perpendicular d do ponto O.
Passo 2
Agora iremos calcular a componente horizontal da força P
Calculando a componente vertical da força P
Passo 3
Partindo do diagrama, calcularemos o momento da força P em relação a O
Iremos considerar os momentos no sentido horário como negativos e os momentos no sentido anti-horário como positivos.
Substituindi
Onde, o sinal positivo indica que o momento resultante é direcionado no sentido anti-hórario.
Portanto, o momento da força em relação a O é .
Passo 4
Vamos escrever a equação para os momentos causados pela força P.
Substituindo
Portanto, a distância perpendicular de O à linha de ação de P é de .
Resposta
- Portanto, o momento da força em relação a O é .
- Portanto, a distância perpendicular de O à linha de ação de P é de .