Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 62

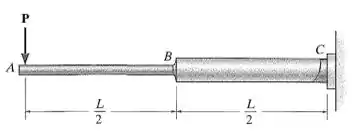
A haste é composta por dois eixos para os quais o momento de inércia de AB é I e de BC, 2I. Determine a inclinação e a deflexão máximas da haste devido à carga. O módulo de elasticidade é E.

Passo 1

Primeiramente, vamos pegar o intervalo 0 ≤ x 1 ≤ L 2 . A equação do momento nesse intervalo será:

M x 1 = - P x 1

Logo:

E I d 2 v 1 d x 1 2 = - P x 1

Integrando 2 vezes, teremos:

E I d v 1 d x 1 = - P 6 x 1 3 + C 1 x 1 + C 2

Agora, pegaremos o intervalo L 2 ≤ x 2 ≤ L :

M x 2 = - P x 2

Logo:

2 E I d 2 v 2 d x 2 2 = - P x 2

Integrando 2 vezes, teremos:

E I d v 1 d x 1 = - P 6 x 2 3 + C 3 x 2 + C 4

Passo 2

As condições de contorno serão:

x 1 = L → v 2 = 0 → d v 2 d x 2 = 0

x 1 = x 2 = L 2 → d v 2 d x 2 = d v 1 d x 1 → v 1 = v 2

Logo:

C 1 = 5 16 P L ²  

C 2 = - 3 16 P L 3

C 3 = P L 2 2

C 4 = - 1 3 P L ³  

Logo, para x 1 = 0 :

θ m á x = 5 P L ² 16 E I

∆ m á x = - 3 P L 3 16 E I

Resposta

θ m á x = 5 P L ² 16 E I

∆ m á x = - 3 P L 3 16 E I

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga A C B , a rigidez flexional é E I na porção AC e n E I na porção CB. Para o carregamento mostrado, determinar a deflexão no ponto C, para: n = 1 / 3
Para a viga A C B , a rigidez flexional é E I na porção AC e n E I na porção CB. Para o carregamento mostrado, determinar a deflexão no ponto C, para: n = 1
Para a viga com o carregamento mostrado, determinar:A declividade no ponto D
Para a viga com o carregamento mostrado, determinar:A deflexão no ponto B
Para a viga com o carregamento mostrado, determinar:A declividade em A;