Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 2.8 - Ex. 5ii

Idem para os arcos representados que se seguem:

Passo 1

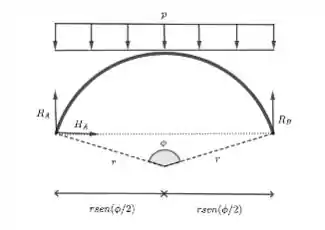
Temos uma reação horizontal e uma vertical no ponto A. No ponto B, temos somente uma reação vertical, que está a uma distância 2   r   s e n   ( ϕ / 2 ) de A. Além disso, temos uma força uniformemente distribuída num intervalo de 2   r   s e n   ( ϕ / 2 ) . Assim, essa força é equivalente a 2   p   r   s e n   ( ϕ / 2 ) atuando no ponto central do sistema, ou seja, x = r     s e n   ( ϕ / 2 ) .

Passo 2

Como não temos outras forças atuando na horizontal, ∑ F X = 0   ⇒ H A = 0 . Além disso, temos

∑ M A = R B ⋅ 2   r   s e n   ( ϕ / 2 ) - 2   p   r   s e n   ( ϕ / 2 ) ⋅ r     s e n   ( ϕ / 2 ) = 0  

⇒ R B =   p r     s e n   ( ϕ / 2 )

∑ F Y = R A + R B - 2   p   r   s e n   ( ϕ / 2 ) = 0

⇒ R A = - R B + 2   p   r   s e n   ( ϕ / 2 ) =   -   p r     s e n   ( ϕ / 2 ) + 2   p r     s e n   ( ϕ / 2 ) =   p r     s e n   ( ϕ / 2 )

Resposta

H A = 0

R A = R B =   p r     s e n   ( ϕ / 2 )