Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 3.7 - Ex. 6vi

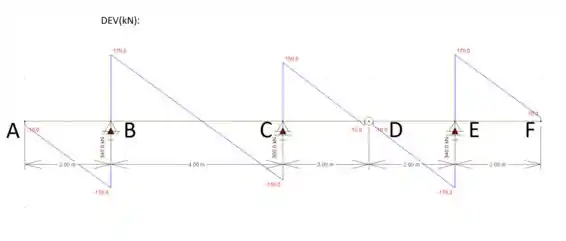
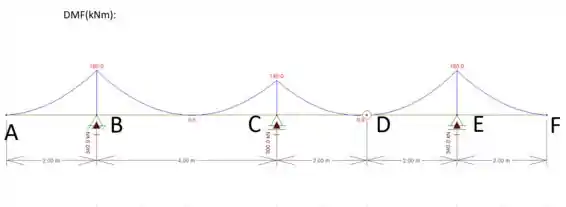
Idem para as vigas Gerber representadas nas figuras que se segue:

Passo 1

Fala ae, pessoal! Tudo blz?

Para resolvermos a estrutura abaixo precisamos identificar quais são os trechos com estabilidade própria (TCEP) e quais são sem estabilidade própria (TSEP).

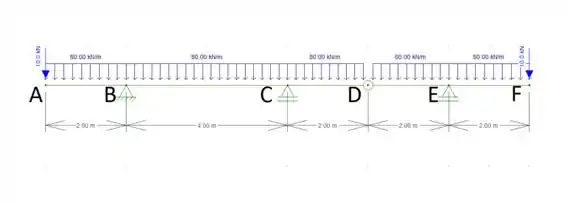
A viga AD é isostática, logo:

T C E P : A D

T S E P : D F

Passo 2

Assim, iremos resolver a viga DF primeiro.

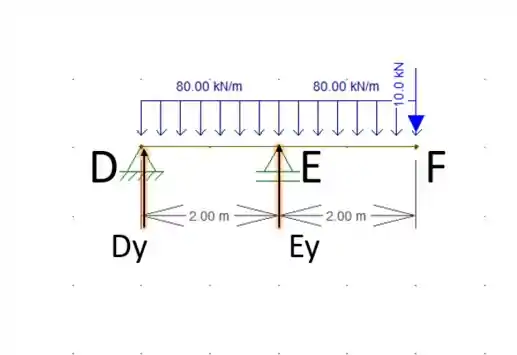
O cálculo das reações de apoio será:

∑ M D → = 0 : ∑ F y → = 0 :

↻ + ∑ M D → = 0 : 2 E y - 80 x 4 x 2 - 10 x 4 = 0

E y = 340   k N ↑

↑ + ∑ F y → = 0 : - 10 - 80 x 4 + 340 + D y = 0

D y = 10   k N ↓

Passo 3

Agora, resolveremos a viga AD, lembrando que D y é um par ação e reação:

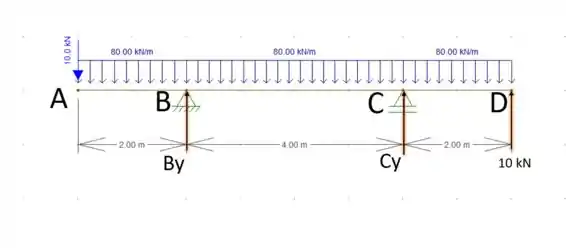
O cálculo das reações de apoio será:

∑ M B → = 0 : ∑ F y → = 0 :

↻ + ∑ M B → = 0 : - 10 x 2 - 80 x 2 x 1 + 80 x 6 x 3 - 4 C y - 10 x 6 = 0

C y = 300   k N ↑

↑ + ∑ F y → = 0 : 300 - 10 - 80 x 8 + 10 + B y = 0

B y = 340   k N   ↑  

Passo 4

Calculando os esforços internos, vindo pela esquerda, temos:

A :   V A = - 10   k N M A = 0

B ( a n t e s ) :   V B = - 10 - 80 x 2 = - 170   k N M B =   - 10 x 2 - 80 x 2 x 1 =   - 180   k N m

B ( d e p o i s ) :   V B = - 170 + 340 = 170   k N M B =   - 180   k N m

C ( a n t e s ) :   V C = 170 - 80 x 4 = - 150   k N M C = - 10 x 6 - 80 x 6 x 3 + 340 x 4 = - 140   k N m

C ( d e p o i s ) :   V C = - 150 + 300 = 150   k N M C = - 140   k N m

D :   V D = 150 - 80 x 2 = - 10   k N M D =   0 ( r ó t u l a )

E ( a n t e s ) :   V E = - 10 - 80 x 2 = - 170   k N M E =   - 10 x 2 - 80 x 2 x 1 = - 180   k N m

E ( d e p o i s ) :   V E = - 170 + 340 = 170   k N M E =   - 180   k N m

F :   V F = 170 - 80 x 2 = 10   k N M F = 0

Passo 5

Entre os pontos BC e DE temos momentos máximos, assim:

M m á x B C = - 10 x 4,125 - 80 x 4,125 x 4,125 2 + 340 x 2,125 = 0,6

M m á x D E = 0,6   ( v i n d o   p e l a   e x t r e m i d a d e   F   o   c á l c u l o   é   i d ê n t i c o   a o   a c i m a )

A partir desses cálculos conseguimos montar nossos diagramas:

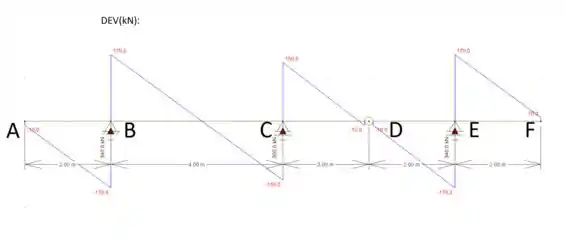
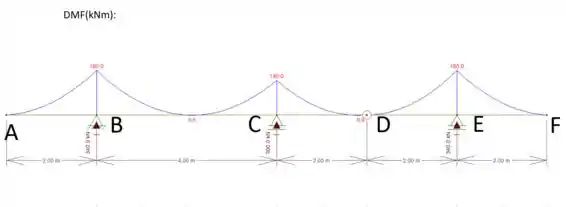
Resposta