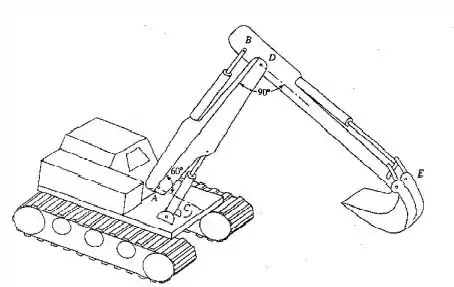
A lança da escavadeira mostrada na Figura 1.73 pode ser aproximada como um tubo de aço com diâmetro externo 10 in, diâmetro interno 9,5 in e comprimento 100 in, com um coeficiente de amortecimento viscose de 0,4. A lança DE pode ser aproximada como um tubo de aço de diâmetro externo 7 in, diâmetro interno 6,5 in e comprimento 75 in, com um coeficiente de amortecimento viscose de 0,3. Estime a constante elástica equivalente e o coeficiente de amortecimento equivalente da escavadeira admitindo que a base AC seja fixa.
Passo 1
Saalve, tudo certo? Bora pra questão sem enrolar! Vamos imaginar a seguinte figura representando o sistema:
Onde temos que a decomposição de y, a posição da garrinha, fica como:
Temos que a tensão equivalente vai ser a soma das tensões de cada mola. Lembra qual a fórmula da tensão pra quando tem coeficiente elástico?? Então me diz aí...
Agora é só aplicar com as molas:
Como já tínhamos encontrado as posições de cada x, vamos substituir:
Cortando os denominadores e os y’s, temos que:
Passo 2
Opa, como já passamos pela teoria e sabemos qual a formulinha que nos dá o coeficiente elástico, vamos substituir os valores dados em cada um deles, de acordo com o que o enunciado nos deu. Bora lá??
Chegou bem até aqui??
Beeeeleza, então bora achar nossa constante elástica equivalente:
Como sabemos que o coeficiente de amortecimento é proporcional ao elástico, podemos usar a mesma proporção e chegamos à: