O motor do Exemplo de Problema 7/2 é mostrado novamente aqui. Se o motor gira em torno do eixo x a uma taxa constante sem rotação em torno do Eixo Z determine a aceleração angular do rotor e do disco à medida que a posição é passada. A velocidade constante do motor é . Também encontre a velocidade e a aceleração do ponto A, que é na parte superior do disco para esta posição.
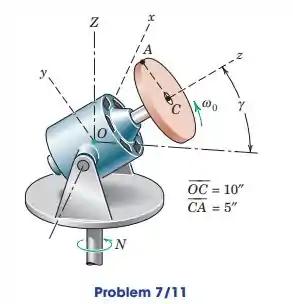
Passo 1
E ai seres de luz, tudo bem?
Bora resolver mais uma?
Encostaaa!!
Já vamos iniciar com os dados fornecidos
Velocidade angular na direção x,
Velocidade constante,
Velocidade angular,
A velocidade angular em z,
Passo 2
A aceleração angular
Vetor posição
Passo 3
Velocidade,
Onde,
Passo 4
A aceleração,