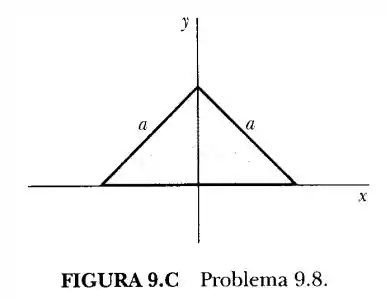
Onde se encontra o centro de massa do triângulo retângulo isósceles de densidade areal uniforme mostrado na Figura 9.C?
Passo 1
E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de dinâmica de um sistema de partículas.
A partir da figura fornecida, por simetria, temos que:
Além disso, por simetria, podemos integrar na metade x > 0 do triângulo para obter:
Ou seja:
Resposta
Ver passo a passo.