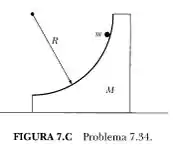
Uma partícula de massa m desliza para baixo de uma cunha circular de massa M como mostra a Figura 7.C. A cunha repousa em uma mesa horizontal lisa. Encontre (a) a equação de movimento de M e m (b) a reação da cunha em m.
Passo 1
Faaaaaala, galera... Tranquileba??
Fazendo um diagrama do esboço dado, temos:
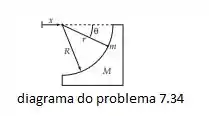
Assim, as coordenadas são:
E para a massinha:
Assim a lagrangiana é:
Note que as coordenadas generalizadas de restrição são
Agora vamos resolver os itens?
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Para a)
Assim, temos e assim, temos:
Onde
Passo 3
Para b)
Podemos pegar a reação da cunha pela equação lagrangiana para r:
Das equações de movimento que obtemos no item a para expressar em termos de e , temos:
Para obtermos uma expressão para , usemos a conservação de energia, ou seja, a hamiltoniana:
Onde é a posição inicial da partícula, e desde que comecemos o repouso (como foi dito) é do a energia do sistema. Integremos a expressão de movimento paara x do item a para obtermos e substituirmos na equação de energia, obtendo assim a expressão para :
Finalmente podemos obter aa expressão em termo de e :
Resposta
Para a)
Onde
Para b)