Uma partícula de massa m está ligada a um suporte rígido por uma mola com constante de força k. Em equilíbrio, a mola se pendura verticalmente para baixo. A esta combinação massa-mola é ligado um oscilador idêntico, sendo que a mola deste último está conectada à massa do primeiro. Calcule as frequências características para oscilações verticais de uma dimensão e compare com as frequências quando uma partícula ou outra se mantiver fixa enquanto as outras oscilam. Descreva os modos normais de movimento para o sistema.

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações acopladas.

O esquema do problema apresentado:

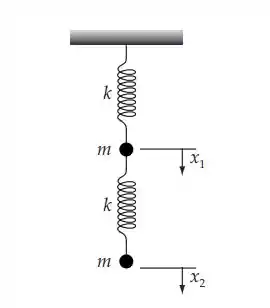
Definimos as coordenadas x1 e x2 como no diagrama. A inclusão da força gravitacional constante para baixo sobre as massas resulta apenas em um deslocamento das posições de equilíbrio e não afeta as frequências próprias ou os modos normais. Portanto, escrevemos as equações do movimento sem os termos gravitacionais:

Assumindo uma dependência harmônica do tempo para x1(t) e x2(t) da maneira usual, obtemos:

Resolvendo, achamos que as frequências próprias são:

Substituindo essas frequências obtemos para o componente autovetor:

Para as condições iniciais , as coordenadas normais são:

Portanto, quando x10 = −1,6180x20, η2(t) = 0 e o sistema oscila no Modo 1, o modo antissimétrico. Quando x10 = 0,6180x20, η1(t) = 0 e o sistema oscila no Modo 2, o modo simétrico.

Quando a massa 2 é mantida fixa, a equação do movimento da massa 1 é:

E a frequência de oscilação é:

Quando a massa 1 é mantida fixa, a equação do movimento da massa 2 é:

E a frequência de oscilação é:

Comparando essas frequências com ω1 e ω2 encontramos:

Assim, o acoplamento dos osciladores produz um deslocamento das frequências para longe das frequências desacopladas, de acordo com a discussão no final da Seção 12.2.

E