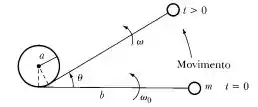
Uma partícula de massa na ponta de um fio leve é enrolada em torno de um cilindro vertical fixo de raio a (Figura 9.F). Todo o movimento ocorre no plano horizontal (despreze a ação da gravidade). A velocidade angular do fio é quando a distância da partícula ao ponto de contato entre o fio e o cilindro é . Determine a velocidade angular e a tensão no fio após este ter se enrolado por um ângulo adicional .

Primeira coisa é colocar a equação da energia cinética, que vai ficar

Simplificando temos que

Agora com a velocidade angular temos

Onde estamos usando com . Para a velocidade depois

Onde temos a velocidade angular, da mesma forma que antes, mas temos que diminuir a velocidade angular do cilindro que agora está rodando também. Como temos

Isolando temos

Para obter a tensão, precisamos olhar a força que atua no sistema. Como o sistema está em rotação, vamos ter uma resultante centrípeta. Então

Mas no caso que temos, do cilindro rodando, temos a rotação do fio. Então, nesse caso vamos ter que

Sendo a variação do raio ou o comprimento do fio que se enrola no cilindro, o raio do fio inicialmente e o comprimento do fio que se enrola no cilindro. Mas, segundo a equação que relaciona e temos

Diferenciando dos dois lados da equação, temos

No nosso caso do cilindro, . Dessa maneira, nossa equação vai ficar

Substituindo essa equação acima na equação da variação do raio, temos

A partir dessa equação, podemos ver que o raio que é a distância que temos vai ser o raio anterior menos o ângulo que o fio se enrolou no cilindro, que é . Assim, vamos ter

Como a resultante centrípeta é a tensão, temos