Um pêndulo se encontra suspenso na cúspide de uma cicloide em um suporte rígido (Figura 3.4). O caminho descrito pelo prumo do pêndulo é cicloidal e fornecido por

Onde o comprimento do pêndulo é e onde é o ângulo de rotação do círculo gerador da cicloide. Demonstre que as oscilações são exatamente isócronas com frequência independente da amplitude.

E aí pessoal, belezinha? Vamos trabalhar agora em algumas questões de oscilações.

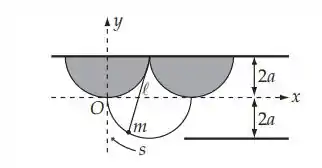
A força responsável pelo movimento do pêndulo é a componente da força gravitacional em m que atua perpendicularmente à parte reta do fio de suspensão. Este componente é visto, na figura abaixo a, como sendo:

Onde α é o ângulo entre a vertical e a tangente à trajetória cicloidal na posição de m. O cosseno de α é expresso em termos dos diferenciais mostrados na figura b como:

Os diferenciais, dx e dy, podem ser calculados a partir das equações definidoras para x() e y() acima:

Logo:

Daí, temos que:

A velocidade do pêndulo é:

Sendo a nova variável, reescrevemos como:

Que é a equação padrão para o movimento harmônico simples:

Logo, ao compararmos, temos que:

E como 4a = l, teremos que:

Assim, o movimento é exatamente isócrono, independente da amplitude das oscilações. Este fato foi descoberto por Christian Huygene (1673).