No problema dos três pêndulos acoplados, considere as três constantes de acoplamento distintas para que a energia potencial possa ser escrita.
![]()
com todos diferentes. Mostre que nenhuma degeneração ocorre neste sistema. Mostre também que a degeneraçáo pode ocorrer apenas se .
Passo 1
Com a expressão dada para , vemos que tem a forma de:
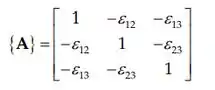
A energia cinética é:
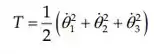
Então é:
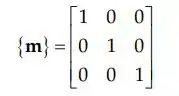
A determinante secular é:
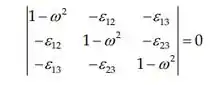
Passo 2
Então:
![]()
Essa equação tem a forma:
![]()
Que terá duas raízes se e somente se:
![]()
Dessa forma a equação do início do Passo 2 terá duas raízes se e somente se:

Resposta
Assim essa equação só é satisfeita se:
![]()
Consequentemente, não haverá degeneração a menos que os três coeficientes de acoplamento sejam idênticos.