Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 14

Um projétil é disparado com velocidade inicial v 0 em um ângulo de elevação α para cima de uma colina com inclinação β ( α > β )

(a) Qual será a distância de aterrissagem do projétil colina acima?

(b) Em qual ângulo α será obtido o alcance máximo?

(c) Qual é o alcance máximo?

Passo 1

E aewww, belezinha?? Você se ligou que já fizemos um problema muito parecido com esse antes? Olha lá o Problema 3. Vamos usar aqui a mesma ideia que usamos lá:

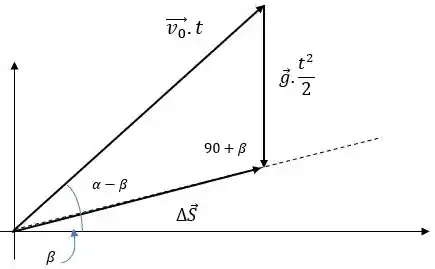
Passo 2

a) Porém, agora, nosso interesse é achar o Δ S , vamos escrever então:

g . t 2 2 sin ⁡ α - β = v 0 . t sin ⁡ 90 + β = Δ S sin ⁡ 90 - α

Mas sabemos que sin ⁡ ( 90 + β ) = cos ⁡ β

E sin ⁡ ( 90 - α ) = cos ⁡ α

Temos então:

t = 2 v 0 g ⋅ sin ⁡ α - β cos ⁡ β

E também:

Δ S = cos ⁡ α cos ⁡ β ⋅ v 0 ⋅ t → Δ S = cos ⁡ α cos ⁡ β ⋅ v 0 ⋅ 2 v 0 g ⋅ sin ⁡ α - β cos ⁡ β

Δ S ( α ) = 2 v 0 2 sin ⁡ α - β cos ⁡ α g c o s 2 β

Passo 3

b) Pra responder a pergunta do problema vamos maximizar a função Δ S ( α )

d d t Δ S α = 0 → 2 v 0 2 g c o s 2 β - sin ⁡ α . sin ⁡ α - β + cos ⁡ α . cos ⁡ α - β cos ⁡ 2 α - β = 0

cos ⁡ 2 α - β = 0 → 2 α - β = π 2

α = π 4 + β 2

Passo 4

c)Substituindo o valor de α encontrado na expressão de Δ S ( α ) e fazendo algumas simplificações, chegamos em:

Δ S M á x = v 0 2 g ( 1 + sin ⁡ β )

Haha, mais uma vez, nosso método de enxergar o lançamento como a composição de um MRU na direção do lançamento, seguido de uma queda livre, se mostrou muuuito eficiente.

CURTIU? deixa seu like e se inscreve no canal... rsrsrsrs 😊

Resposta

a )   Δ S ( α ) = 2 v 0 2 sin ⁡ α - β cos ⁡ α g c o s 2 β

b )   α = π 4 + β 2

c )   Δ S M á x = v 0 2 g ( 1 + sin ⁡ β )

Exercícios de Livros Relacionados

Um projétil é lançado em um fluido experimental no instante t = 0 . A velocidade inicial é v 0 e o ângulo com a horizontal é θ . O arrasto sobre o projétil resulta em um termo de aceleração a D = - k
Um projétil é lançado a partir do ponto A e cai no mesmo nível em D . Sua altitude máxima é h . Determine e represente graficamente a fração f 2 do tempo total de voo em que o projétil está acima do n
Uma bola é jogada para cima com uma velocidade de 5 m/s do topo de um prédio de 10 m de altura. Um segundo mais tarde, outra bola é jogada verticalmente a partir do chão com uma velocidade de 10 m/s.
Uma partícula move-se ao longo de uma curva definida pela equação s=( t ³-3 t ²+2 t ) ³ ² m, onde t é dado em segundos. Trace os gráficos s - t ,v - t e a - t para a partícula em 0≤t≤3 s .
Um míssil partindo do repouso move-se ao longo de uma pista reta e por 10 s tem uma aceleração, como mostrado. Trace o gráfico v-t que descreve o movimento e descubra a distância percorrida em 10 s.