Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Dinamica Classica de Particulas e Sistemas - Marion- Ed: 5º - Capítulo 2.Problemas - Ex. 10

Repita o Exemplo 2.4 efetuando um cálculo no computador para resolver a equação 2.22. Use os valores a seguir: m = 1 k g , v 0 = 10 m / s , x 0 = 0 e k = 0,1 s - 1 . Elabore gráficos de v versus t , x versus t e v versus x . Compare com os resultados do Exemplo 2.4 para verificar se os seus resultados são razoáveis.

Passo 1

Fala pessoal, tudo blz? Essa questão aí, na verdade já está resolvida no exemplo 2.4, a única coisa que temos que fazer aqui é uma análise de valores com o computador, então vamos lá.

m d v d t = - k m v

Resulta em:

ln ⁡ v = - k t + ln ⁡ v 0

v = v 0 ⋅ e - k t

x t = v 0 ∫ e - k t  

Com os valores fornecidos:

v t = 10 e - t / 10

x t = 100 ( 1 - e - t / 10 )

v x = 10 - x 10

Passo 2

Vamos plotar esses gráficos no Geogebra para ver como eles se comportam.

Plotando y = 10 e - x / 10

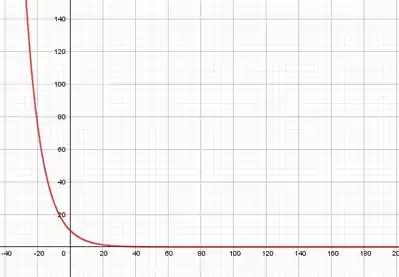
Passo 3

Agora y = 100 ( 1 - e - x / 10 )

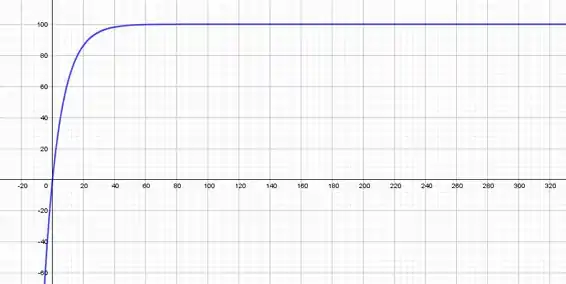
Como já esperávamos, o comportamento do gráfico nos mostra que para:

t → ∞ temos x t → 100

Passo 4

Agora y = 1 0 - x 10

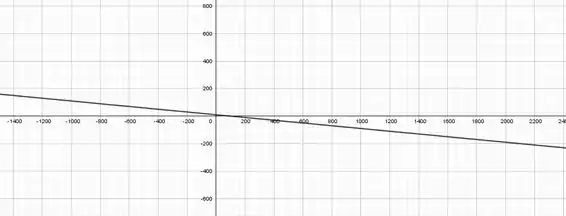
Resposta

Ver gráficos.