Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 9.Problemas - Ex. 105b
Resolver o , considerando que a barra de diâmetro igual a seja substituída por outra de de diâmetro e de mesmo comprimento.
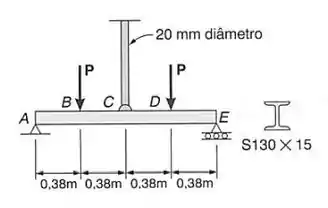
Passo 1
Sabemos que o ponto C também sofre a deformação em uma barra linear, e para isso é bem simples fazer a conta, olhando a tração que age na nossa barra, tem-se que:
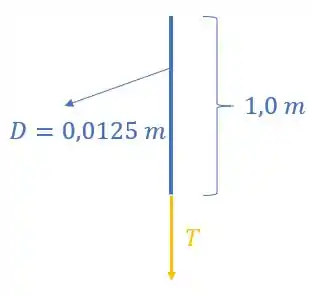
Sabe-se que:
Passo 2
Como as deformações no ponto C precisam ser iguais, temos que:
Sabe-se que:
Passo 3
Agora precisamos determinar os momentos nos pontos B e C da viga, e para isso, precisamos carregar a nossa viga com a carga de tração que temos, assim, teremos que:
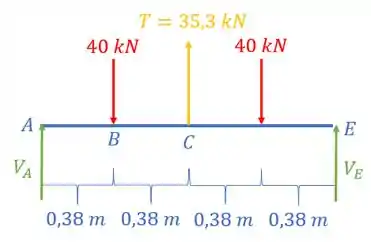
Calculando as reações de apoio, tem-se que:
Com a reação de apoio, da pra calcular o momento em B, assim, tem-se que:
Resposta
Exercícios de Livros Relacionados
Para a viga com o carregamento do Prob.9.95, determinar:Quanto o ponto B deverá ser levantado, se a deflexão em CF deve ser de 10mm para baixo, em relação à horizontal que passa por A;A reação em B de
Para a viga com o carregamento mostrado, determinar:O valor de a para que a declividade na extremidade A seja zero;A correspondente deflexão no ponto C.
Para a viga com o carregamento mostrado, determinar:O valor de a para que a declividade na extremidade A seja zero;A correspondente deflexão no ponto C.
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Para P = 360k N , determinar:A reação em BA declividade em BA deflexão em AUsar E = 200G P a
Antes da carga P ser aplicada, uma abertura δ 0 = 5 m m existe entre a viga e o apoio em B. Sabendo-se que E = 200G P a , determinar:a intensidade P da carga para que a deflexão em A seja zero.A corre