Um satélite da Têrra tem perigeu de 300 km e apogeu de 3.500 km sobre a superfície do planeta. Qual será a distância do satélite acima da Terra quando (a) ele tiver girado 90° em torno da Terra a partir do perigeu e quando (b) ele tiver se movido meio caminho entre o perigeu e o apogeu?
Passo 1
Faaaaaala, galera... Tranquileba??
para a)
Um esboço do que o enunciado nos diz é:
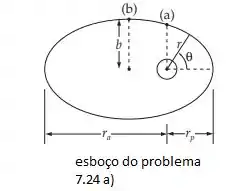
Com o centro da Terrana origem, a equação de orbita como já sabemos é:
Também é nos dito no livro que:
Bora pro próximo passo?!
Passo 2
Obrigado por vir.
Assim:
quando de forma que:
Assim, da equação 0.1 nós obtemos que
Assim a equação de orbita é:
Como dito
Passo 3
Para b)
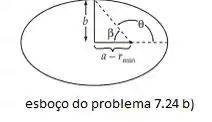
Observe que:
Usando
Substituindo esse valor de na equação 0.1:
O que é 1900 km acima da Terra.
Resposta
Para a)
Para b)
O que é 1900 km acima da Terra.