Para o sistema mostrado na Figura 6.33:
- Determine o polinômio característico
- Construa um gráfico para considerado a
- Determine
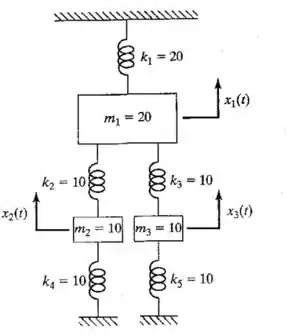
Passo 1
Falaaa meus amigos! Como vocês estão? Vamos pra mais uma questãozinha desse assunto? Então, se liga. Aqui a grande jogada é fazermos a matriz de elasticidade para os três casos das forças, anulando duas delas e destacando uma para a matriz. Se liga:
Seja:
Logo,
Agora fazemos isso para os outros dois .
Seja:
Logo,
Seja:
Logo,
Passo 2
A partir disso, a gente já pode montar a matriz com os valores de que a gente achou! Só bora! A gente tem a seguinte matriz:
E para a matriz de massa:
A partir disso tudo, a gente já pode achar o nosso polinômio característico de:
Passo 3
A partir da regra de polinômio característico:
Calculando o determinante:
Logo:
Passo 4
Plotando esse polinômio, a gente tem algo parecido com isso:
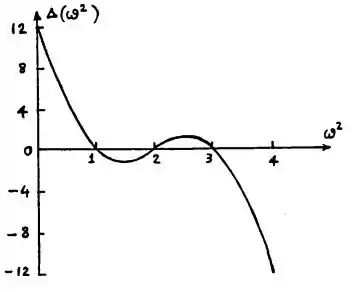
E por fim, no item c), as raízes da equação a gente acha pelo gráfico mesmo, bastando olhar aonde o gráfico toca o eixo de . Logo:
Resposta
a)
b)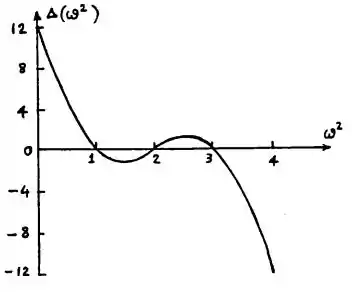
c)