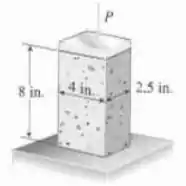
Um tijolo padrão (dimensões ) é comprimido por uma força , como ilustrado na figura. Se a tensão última de cisalhamento para o tijolo é e a tensão última de compressão é , qual o valor da força para quebrar o tijolo?

Bora lá galera!

Primeiro vamos calcular a área em que a força está exercendo a compressão

Além disso, a tensão última é quando se atinge a máxima força que pode ser aplicada ao corpo de prova. Com isso, temos que:

(tensão última de compressão)

(tensão última de cisalhamento)

Sabe-se que a carga de compressão tem Tensão normal máxima definida por

Eq. (1)

E a Tensão de cisalhamento máximo é definida por

Eq. (2)

De acordo com o enunciado, a tensão última de cisalhamento para o tijolo é e a tensão última de compressão é . Com isso, como a tensão de cisalhamento é menor do que a metade da tensão normal admissível, a tensão de cisalhamento é quem será a crítica.