Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Estatica das Estruturas por Humberto Lima Soriano- Ed: 3º - Capítulo 4.9 - Ex. 4ii

Trace os diagramas dos esforços seccionais dos pórticos com regiões fechadas representados nas duas próximas figuras.

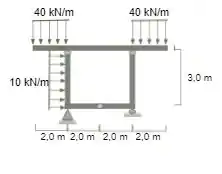ii.

Passo 1

E aí.....tudo belezinha?

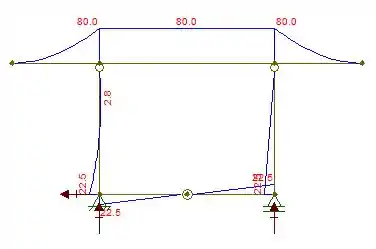
Para começarmos esta questão devemos analisar as reações de apoio da estrutura e separá-las em estruturas isostáticas equilibradas que permitam os cálculos, logo abaixo podemos ver as estruturas separadas e as reações aplicadas.

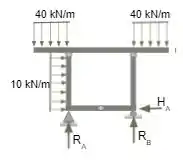
Agora podemos calculas o valor de R A e R B de acordo com o equilíbrio da parte de cima do pórtico, considerando as reações de equilíbrio.

∑ F x = 0 → ∑ F x = H A - 10 → H A = 10 k N

∑ F y = 0 → ∑ F y = R A + R B - 40 . 2 - 0 - 40 . 8 - 6 → R A + R B = 160 k N

∑ M = 0 → ∑ M = R B . 6 - 2 - 40.8 . 0 + 2 2 - 40 . 8 . 6 + 8 2 → 4 R B = 320   k N → R B = 320 4 = 80 k N

Substituindo o valor de R B na equação associada ao equilíbrio de forças horizontais, temos:

R A + R B = 160 → R A = 160 - 80 = 8 0 k N

Com estas informações agora podemos construir o diagrama de força normal, já que este diz respeito as forças sobre a peça.

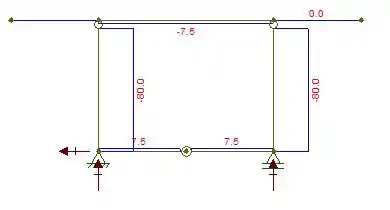
Passo 2

Para construir os diagramas de esforço cortante, devemos fazer os balanços verticais por seção, indo de 0 até a seção. Considerando V(x) o valor do esforço cortante na posição x e sendo representado pelas flechas na imagem abaixo.

∑ F y + V x = 0

Considerando a seção 1, 0 ≤ x ≤ 2 , da viga, temos:

∑ F y + V ( x ) = 0 → 40 . x - 0 - V x = 0 → V x = - 4 0 . x

Já para a segunda parte da seção, 2 ≤ x ≤ 6 , temos:

∑ F y + V x = 0

Para a última seção da viga ( 6 ≤ x ≤ 8 ) , temos

∑ F y + V x = 0 → - 4 0 . x - 0 + R A + R B - V x = 0 → V x =   - 4 0 . x + 32 0

Como temos um pórtico, devemos realizar o mesmo passo para as paredes do pórtico. Neste caso, temos somente uma seção 0 ≤ x ≤ 3 , sendo assim:

∑ F y + V x = 0 → 10 ( x - 0 ) + V x = 0 → V x = - 1 0 . x k N

No outro lado do pórtico temos a mesma condição, porém com as forças contrárias sendo assim a equação do diagrama de força cortante, será a mesma, porém com o sinal invertido.

∑ F y + V x = 0 → - 10 ( x - 0 ) + V x = 0 → V x = 10 . x k M

Sendo assim o diagrama de forças, será:

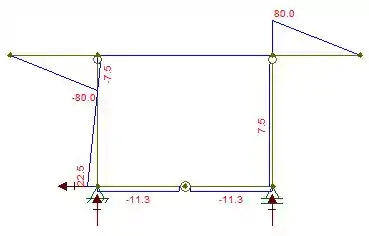
Passo 3

Para realizar o diagrama de momento fletor, temos que fazer o balanço de momento em cada seção, em que M(x) é o valor do momento em x, ou seja:

∑ F y x - x c a r g a + ∑ M + M x = 0

  • Assim como antes começaremos pela viga do pórtico, definindo a primeira seção como 0 ≤ x ≤ 2 ) ;

    • ∑ M + M x = 0 → 40 2 . x - 0 2 + M x = 0 → M x = - 20 x 2

  • Agora na segunda seção ( 2 ≤ x ≤ 6 )

∑ M + M x = 0 → + 40 . x - 0 2 + 40 . ( x - 0 ) + M x = 0

M ( x ) = 8 0 k N

Assim como no diagrama de esforça cortante, temos que realizar também os da parede, como uma só seção ( 0 ≤ x ≤ 3 ) .

- F + M x = 0 → - 10 x - 0 . x - 0 3 + M x = 0 → M x = - 10 . x 2

No outro lado do pórtico temos a mesma condição, porém com as forças contrárias sendo assim a equação do diagrama de força cortante, será a mesma, porém com o sinal invertido.

- F + M x = 0 → - 10 x - 0 . x - 0 3 + M x = 0 → M x = - 10 . x 2

E agora, bora para a próxima questão =)

Resposta

Ei, a resposta está no passo a passo :)