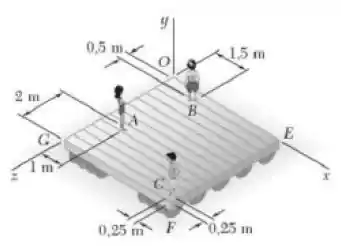
Três crianças estão em pé sobre uma balsa de . Os pesos das crianças nos pontos e são de , e , respectivamente. Se uma quarta criança de peso subir na balsa, determine onde ela deve ficar se as outras crianças permanecerem nas posições mostradas na figura e a linha de ação da resultante dos quatro pesos passar através do centro da balsa.

Oi pessoal, tudo bem? Vamos analisar essa questão.

Sabemos que a resultante é a soma das quatro forças que representam os pesos das crianças, portanto:

Seja a distância da criança no eixo e a distância da criança no eixo .

Para determinarmos a distância , igualaremos o momento em torno do eixo para ambos os sistemas equivalentes apresentados no item anterior:

Resolvendo, temos que: