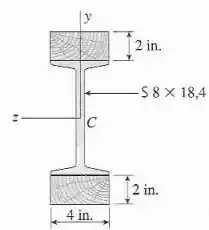
Uma viga simples que tem de comprimento sustenta uma carga uniforme de intensidade . A viga é construída de uma seção (perfil I) reforçada com vigas de madeira que estão seguramente vinculadas aos flanges (veja a seção transversal ilustrada na figura). As vigas de madeira têm de profundidade e de largura. O módulo de elasticidade do aço é 20 vezes o da madeira. Se as tensões admissíveis no aço e na madeira são e , respectivamente, qual é a carga admissível ? (Nota: Desconsidere o peso da viga e veja a Tabela E.2 do Apêndice E para as dimensões e propriedades da viga de aço.)
Passo 1
- Viga de aço
- Viga de madeira
- Tabela E.2 do Apêndice E
Bora lá galera!
Primeiro vamos transformar a seção para um único material. O enunciado nos diz que o módulo de elasticidade do aço é 20 vezes o da madeira, logo:
Com isso, o momento de inércia da seção transformada fica:
Passo 2
Agora vamos calcular os momentos máximos com relação a cada material.
- Momento máximo – aço
- Momento máximo – madeira
Equação 6.15
Isolando o momento, temos que:
Equação 6.17
Isolando o momento, temos que:
Portanto, como , o
E com isso, para calcularmos a carga admissível , aplicamos na seguinte equação:
Isolando a variável e substituindo os valores numéricos, temos que: