Uma amostra de 200 habitantes de uma cidade foi escolhida para declarar sua opinião sobre um certo projeto governamental. O resultado foi o seguinte:

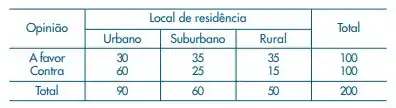
(a) Calcule as proporções em relação ao total das colunas.

(b) Você diria que a opinião independe do local de residência?

(c) Encontre uma medida de dependência entre as variações.

(b) Você diria que a opinião independe do local de residência?

Primeiro, vamos montar uma tabelinha com os valores esperados.

Com base nos valores observados e esperados, vamos encontrar nossa medida de dependência entre as variáveis, ou seja, o .

Se a hipótese de não-associação for verdadeira, o valor calculado de deve estar próximo de zero. Se as variáveis forem associadas, o valor de χ2 deve ser grande 😉.

• Cálculo das frequências esperadas

Considere a tabela com os valores observados e esperados:

Calculando o qui-quadrado:

Calculando o Coeficiente de Contingência de Pearson:

Como é grande parece haver associação entre as variáveis. Logo, a opinião parece depender do local de residência do indivíduo.

(c) Encontre uma medida de dependência entre as variações.

Já encontramos é o 😉.