Uma amostra de 20 garrafas de certo tipo de vidro foi selecionada e a resistência à pressão interna de cada garrafa foi determinada. Considere as seguintes informações parciais da amostra: mediana = 202,2 quarto inferior = 196,0 quarto superior = 216,8 Três observações menores 125,8 188,1 193,7 Três observações maiores 221,3 230,5 250,2
a. Há algum outlier na amostra? Algum outlier extremo?
b. Construa um boxplot que mostre outliers e comente suas características
Passo 1
Saaaalve, tranquilo? Vamos lá resolver mais uma questão juntos?! 😊
- Suponha que temos n Observações. Ordenando a observação de menor para maior e dividindo as duas metades (metade menor metade/maior, se n é estranho a mediana está incluído em ambas as metades) definimos o quarto baixo como a mediana da menor metade e do quarto superior como a mediana da maior metade. Quarta propagação é definido como
- O boxplot é baseado nos cinco números:
Passo 2
Observações maiores do que do quarto mais próximo(superior/inferior) é um outlier. Se o outlier é maior do que a partir do quarto mais próximo, dizemos que é um extremo outlier, caso contrário, é um outlier moderado.
Temos que
Usando isso, podemos calcular os limites para os outliers leves e extremos. Denotar
Moderada outliers são todos os valores entre 133.6 e 164.6 bem como entre 248 e 279.2.
O extremo outliers são todos os valores menores do que 133.6 e maior do que 279.2.
Há um outliers extremos nas observações listadas e 125.8 porque é menor do que 133.6.
Há um leve outlier 248 250.2
Passo 3
menor , quarto, quarto inferior, médio, quarto superior, maior ,
As linhas para a parte superior e inferior do boxplot são os menores/maiores valores, a linha no boxplot representa a mediana, os outliers são pontos e a caixa começa na quarta inferior e termina em quarto. A partir do boxplot podemos notar que ele é positivamente distorcido (a mediana é mais para a esquerda).
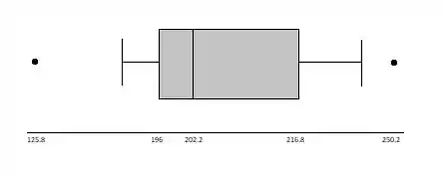
Resposta
- Outlier extremo = 125.8, leve outlier = 250.
- Ver o gráfico