Exercícios de Introdução à Estatística - Lista de Exercícios Resolvida

João, professor de probabilidade, está realizando uma pesquisa e gostaria de calcular o número de amostras possíveis que se pode obter a partir de uma população de 20 elementos se quisermos montar uma amostra aleatória com elementos sem reposição.

Uma população se encontra dividida em três estratos, com tamanhos, respectivamente, , e . Ao realizar uma amostragem estratificada proporcional, doze elementos da amostra foram retirados do primeiro estrato. Qual o número total de elementos da amostra?

Suponha que temos uma população de elementos, e queremos montar uma amostra usando um elemento a cada elementos da população, a partir do elemento. Que tipo de amostragem devemos fazer? Qual deve ser a nossa amostra?

1. Defina população e amostra. Dê exemplos.

Um administrador hospitalar faz uma pesquisa com as pessoas que estão na fila de espera para serem atendidas pelo sistema SUS.

1. Se para realizar esta pesquisa, o administrador resolve entrevistar uma a cada 10 pessoas da fila, que tipo de amostragem ele realizou?
2. As pessoas desta fila foram divididas em três grupos, de acordo com sua doença, cujos tamanhos são, respectivamente, e sabendo que, ao ser realizada uma amostragem estratificada, nove elementos da amostra foram retirados do terceiro grupo, determine o número total de elementos da amostra, ou seja, o número total de pessoas entrevistadas.

O Banco XXL emprega os seguintes planos amostrais a depender da finalidade:

Plano 1) Ele se preocupa com a qualidade do serviço oferecido. Para isto, sempre entrevista o terceiro cliente para cada grupo de 50 clientes que se dirigem ao banco nas segundas, quartas e sextas-feiras;

Plano 2) Ele quer lançar um novo tipo de cartão de crédito e quer saber se seus clientes irão aderir ou não. Para isto, ele sorteou um número aleatório entre e , obtendo-se o número dez e seguiu-se entrevistando o décimo cliente em cada grupo de da lista de clientes.

Plano 3) O banco quer abrir uma agência da cidade Santo Antonio de Borá e quer ter uma estimativa de possíveis clientes domiciliados neste município. O município tem quarteirões. Selecionaram-se 30 quarteirões aleitoriamente e todos os domicílios do quarteirão foram entrevistados.

Plano 4) O banco quer estudar o perfil dos clientes. Ele tem agências espalhadas pelo país. De cada agência uma amostra aleatória de clientes foi selecionada.

Plano 5) O banco quer lançar um novo fundo de investimento para todos os clientes. Para isto ele enviou um questionário por e-mail para o titular da conta dos melhores clientes segundo um critério de classificação criado pela equipe econômica. Baseado nos resultados dos questionários devolvidos o banco decidirá se vai lançar o fundo ou não.

De acordo com a descrição, estes planos amostrais podem ser classificados respectivamente como:

O que vem a ser um “estimador” e uma “estimativa” de um parâmetro.

b) Seja , “” observações de uma v.a. “”. Qual a condição que estas observações devem satisfazer para que ela seja considerada uma amostra aleatória?

Seja , observações de uma v.a. . Qual a condição que estas observações devem satisfazer para que ela seja considerada uma amostra aleatória?

Suponha que um dado honesto seja rolado duas vezes. Quais são os possíveis valores que as seguintes variáveis aleatórias podem assumir e qual a distribuição de probabilidade associada à cada uma delas?

a) O máximo valor que aparece nas duas vezes em que o dado é jogado.

b) O valor da primeira jogada subtraído do valor da segunda jogada.

De um grupo de calouros, alunos do segundo ano, alunos do terceiro ano e formandos, forma-se aleatoriamente um comitê de pessoas. Determine a probabilidade de que o comitê seja formado por:

a) (dois) alunos do segundo ano e (dois) alunos do terceiro ano;

b) apenas alunos do segundo ou terceiro ano;

Dois times de vôlei feminino: Osasco e SESI disputam a final da Superliga de Vôlei Feminino numa série de até jogos (Será campeão o time que ganhar jogos). Se a probabilidade de vitória é a mesma para as duas equipes, determine a probabilidade de:

a) O campeão sair em até seis jogos.

b) O campeão sair em seis jogos, se o time Osasco venceu os dois primeiros jogos.

Em uma linha de produção de uma fábrica, três peças fabricadas serão sorteadas sequencialmente, sem reposição e inspecionadas. Cada peça será classificada como defeituosa (D) ou não defeituosa (N).

a) Descreva o espaço amostral associado a este experimento.

b) Qual a probabilidade de obtermos mais que das peças defeituosas?

c) Se sortearmos sequencialmente um número par de peças, em quantos resultados podemos obter pelo menos as primeiras peças defeituosas?

Um comprador, ao receber de um fornecedor um grande lote de peças, decidiu inspecionar delas. Decidiu, também, que o lote será rejeitado se ficar convencido, ao nível de de significância, de que a proporção de peças defeituosas no lote é superior a . Qual será sua decisão (rejeitar ou não rejeitar o lote) se na amostra foram encontradas onze peças defeituosas? Apresente as hipóteses, a regra de decisão e sua conclusão.

1. Numa empresa, a diretoria avalia que a probabilidade de que o Engenheiro “cadastro A157” conclua certo projeto em tempo hábil é de , enquanto que a estima valendo para o colega engenheiro “cadastro A180”. A chefia resolve que os dois devem tentar concluir o projeto independentemente, visando aumentar as chances de sucesso. Qual a probabilidade do projeto ser concluído neste caso? É válida a estratégia?

1. Defina população e amostra. Dê exemplos.

Dadas as seguintes informações;

Um por cento das mulheres tem câncer de mama.

Noventa por cento das mulheres que têm câncer de mama testam positivo em mamografias.

Oito por cento das mulheres terão falsos positivos.

a) Qual a probabilidade de uma mulher obter o resultado positivo para câncer de mama?

b) Qual é a probabilidade de uma mulher ter câncer se ela tiver um resultado positivo na mamografia?

Os cursos de Engenharia de Alimentos, Engenharia Naval e Engenharia de Minas têm as seguintes porcentagens de rapazes, respectivamente: e . Um desses três cursos é selecionado ao acaso e oito alunos são escolhidos, com reposição. Se o resultado for ( para rapaz e para moça):

a) Qual a probabilidade de ocorrer dado que vem de Engenharia de Alimentos? Qual a probabilidade de ocorrer dado que vem de Engenharia Naval? Qual a probabilidade de ocorrer dado que vem de Engenharia de Minas?

b) Qual é a probabilidade de ter sido selecionado “Engenharia de Minas”?

Uma companhia de seguros, que trabalha no ramo de automóveis, investigou a relação entre o hábito de fumar do motorista do carro e a frequência das reclamações relativas a acidentes com danos materiais. Para isso, considerou-se as variáveis aleatórias:

número de acidentes sofridos pelo motorista (a companhia considerou de um a três acidentes) e:

Suponhamos que a companhia obteve que a distribuição conjunta de e é dada por:

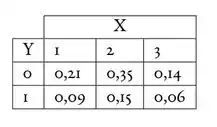
a) Determine as distribuições marginais de e

b) Podemos afirmar que o número de acidentes sofridos pelo motorista independe do fato desse ser ou não fumante?

c) Qual a probabilidade do motorista ser fumante dado que ele sofreu pelo menos dois acidentes?

Humberto deseja aumentar a capacidade de memória RAM do seu microcomputador. A placa mãe do PC de Humberto permite a instalação de até quatro pentes de memória e atualmente só possui um pente. Ele vai a uma loja e solicita a compra e instalação de mais três pentes de memória idênticos ao atual. Na loja há pentes com essa característica. O que Humberto não sabe, e o técnico também não, é que entre os pentes disponíveis há quatro pentes defeituosos. Se os três novos pentes forem escolhidos ao acaso (sem reposição), informe:

a) Qual o espaço amostral associado a qualidade dos três pentes de memória adquiridos?

b) Qual a probabilidade de que a capacidade de memória do PC realmente aumente? Sugestão: Determine o número de escolhas de pentes defeituosos extraídos do lote.

Observe as seguintes representações de dois grafos G e H e responda.

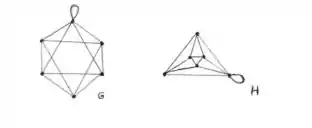
a)G é um grafo simples ou multigrafo? Justifique.

b)G e H são grafos isomorfos? Justifique.

c)Qual é a definição de grafo euleriano? Existe uma condição necessária e suficiente para sim? (Se sim descreva).

d)G é euleriano? Se sim, exiba a estrutura que satisfaz a definição, senão justifique.

e)G é bipartido? Justifique.

f)G é planar? Justifique.

g)Enuncie o Teorema de Euler que dá uma condição necessária para todo grafo planar.

h)Defina árvore

Defina população e amostra. Dê exemplos.

Defina população e amostra. Dê exemplos.

Parzival é um famoso jogador de um popular jogo online. É sabido que sua pontuação por partida desse jogo segue uma distribuição Normal com média de pontos e desvio padrão de pontos. Se, em uma partida, ele consegue pontuação superior a , ele ganha um item (prêmio) raro no jogo; e se consegue pontuação entre , ele ganha um item comum.

(a) Qual é a probabilidade de Parzival ganhar um item raro em uma partida? E qual é a probabilidade de ele ganhar um item comum?

(b) Sabendo que em uma partida Parzival não ganhou o item raro, qual é a probabilidade de ele ter ganhado o item comum?

(c) Acima de qual valor estão das melhores pontuações de Parzival?

Dois dados estão dentro de uma urna. Ambos os dados são honestos (a probabilidade de sair cada uma das faces é a mesma), porém, enquanto o primeiro dado (dado 1) tem as faces numeradas de 1 a 6, o segundo dado (dado 2) tem duas faces de número 1, duas faces de número 2 e duas faces de número 3. Um dos dados é selecionado ao acaso e retirado da urna. Responda às seguintes questões:

(a) Se o dado selecionado é lançado uma vez, qual é a probabilidade de sair face de número 2?

(b) Se o dado selecionado é lançado duas vezes, qual a probabilidade da soma das faces (dos dois lançamentos) ser menor ou igual a 3?

(c) Se o dado é lançado três vezes, obtendo três vezes a face de número 1, qual é a probabilidade do dado selecionado ter sido o dado 1?

O escore final num exame de proficiência na língua inglesa varia de pontos, pulando de dez em , com mais pontos indicando um melhor desempenho. Informações coletadas durante várias aplicações deste exame ao longo de anos permitem estabelecer o seguinte modelo para o desempenho no teste:

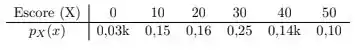
(a) Qual o valor de para que seja de fato uma função de probabilidade?

(b) Algumas universidades americanas exigem um escore mínimo de pontos para aceitar candidatos de países de língua não inglesa. Numa amostra aleatória de estudantes dentro de um grupo grande de alunos, calcule a probabilidade de pelo menos consigam satisfazer o requisito.

(c) Dentre os candidatos que realizam o teste, em geral pretendem usar o resultado em apenas uma universidade. Usando o modelo Poisson de forma aproximada, calcule a probabilidade de que numa amostra de candidatos, sorteado de forma aleat ́oria, no mínimo usarão o resultado do teste em apenas uma universidade.

Seja o vetor aleat ́orio bidimensional , os valores possíveis tanto de quanto de pertencem a . Sabe-se que a probabilidade conjunta, é tal que:

Calcule:

(a) os valores esperados, e também as variâncias, ;

(b) a covariância, São variáveis aleatórias independentes?

(c) a função de probabilidade condicional de dado que , ou seja .

Suponha que deseja-se estimar a proporção de indivíduos que votam em um determinado candidato em uma eleição. Uma amostra de pessoas foi obtida, e, destas pessoas, disseram votar no tal candidato.

Obtenha:

(a) O máximo Erro Quadrático Médio () que pode ser obtido para o estimador

da proporção de votos no candidato em questão, em que ́é o número de votos favoráveis ao candidato na amostra, e é o tamanho da amostra.

(b) O intervalo de confiança conservativo para , com coeficiente de confiança de .

(c) O tamanho da amostra para que o erro da estimativa não exceda a unidades com probabilidade de

A largura dos ombros de pessoas é uma v.a. Normal de média e desvio padrão de . Pretende-se dimensionar o corredor de uma casa, de forma a permitir a passagem de duas pessoas, de maneira confortável. Considera-se preenchida as condições de conforto quando há uma folga de entre os ombros de pessoas e entre os ombros e as paredes.

(a) Um projetista desenhou o corredor com de largura; qual a probabilidade da passagem se dar de maneira confortável?

(b) Que largura deve ter o corredor para permitir, em dos casos, a passagem de duas pessoas, ocorra de maneira confortável?

Estações de monitoramento mediram a concentração partículas inaláveis de

e a temperatura média mensal (em graus C) para cada mês de um dado ano em uma cidade. Os dados medidos seguem abaixo:

Use que

1. Construa o boxplot da concentração de PM10 e interprete-o quanto a simetria e valores discrepantes.
2. Usando uma medida de variabilidade adequada, compare os níveis de PM10 e a temperatura média.

(c) Obtenha a reta de regressão e interprete as estimativas dos coeficientes.

Uma fábrica produz peças de metal que possuem cobre em sua composição. É sabido que a quantidade de cobre em cada peça segue uma distribuição normal com média de quando o processo de produção está sob controle. Se a média for diferente, o processo é dito estar fora de controle. Periodicamente, para fins de verificação do processo de produção, uma amostra aleatória de 10 peças é coletada e o nível de cobre é medido. Na verificação mais recente, obteve-se média amostral de e desvio padrão amostral de

(a) Ao nível de de significância, pode-se dizer que o processo está sob controle? Especifique formalmente as hipóteses, o critério de teste e comente suas conclusões.

(b) Para o teste acima, o p-valor seria maior ou menor que ? Explique.