Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 13.Exercícios - Ex. 41

Um artigo no periódico descreveu um experimento para investigar o efeito da temperatura de secagem do grão de trigo sobre a qualidade do processo de assar pão. Três níveis diferentes de temperatura foram usados e a variável de resposta medida foi o volume de pão produzido. Os dados são mostrados a seguir:

a)A temperatura de secagem afeta o volume médio do pão? Use .

b)Encontre o valor P para esse teste.

c)Use o método MDS de Fisher para determinar quais são as médias diferentes.

d)Analise os resíduos desse experimento e comente a adequação do modelo.

Passo 1

Hey, jovem, tudo bem contigo? Espero que sim 😊 Bora pra mais uma questãozinha de estatística? Vamo que vamo! Então, nessa questão a gente tem que para o item a), os resíduos vao se concentrar no gráfico da seguinte forma:

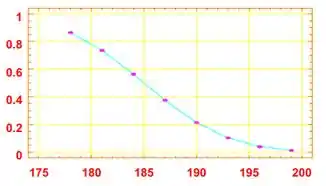
b) Para os resíduos contra y, temos o inverso:

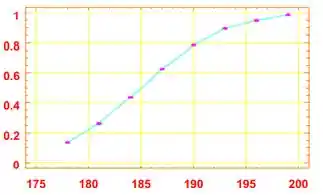
Passo 2

Para o intervalo de confiança, temos que:

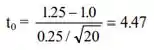
E por fim aplicando MDS de fisher:

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Foram sorteadas 15 famílias com filhos num certo bairro observando o número de crianças de cada família, matriculadas na escola. Os dados foram: 1, 1, 2, 0, 2, 0, 2, 3, 4, 1, 1, 2, 0, 0, e 2. Obtenha

Para estimar a média das alturas (em metros) numa certa população, dois institutos de pesquisa coletaram cada um a sua amostra e usaram estimadores diferentes. Os resultados estão na tabela abaixo:Voc

Considere o CD-Notas e retire uma amostra com reposição de tamanho n = 10. Determine o erro padrão estimado pelo método bootstrap das estatísticas (use B = 15, por exemplo):(a) md = mediana da amostra