Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 14.Exercícios - Ex. 56
Um artigo no periódico Journal of Coating Technology (Vol. 60, 1988, pp. 27-32) descreve um planejamento fatorial usado para estudar uma tinta, à base de prata, para automóveis. A variável de resposta é a propriedade de distinguir imagens (PDI). As variáveis usadas no experimento são
Porcentagem de poliéster por peso de poliéster/melamina (valor baixo=; valor alto=)
Porcentagem de caboxilato butirato acetato de celulose (valor baixo=; valor alto=)
Porcentagem de estearato de alumínio (valor baixo=; valor alto=)
Porcentagem de catalisador ácido (valor baixo=; valor alto=)
As resposta são: ; ; ; ; ; ; ; ; ; ; ; ; ; e .
Estime os efeitos dos fatores.
A partir do gráfico de probabilidade normal dos efeitos, tente um modelo para os dados desse experimento.
Que modelo você usaria para descrever o processo baseado nesse experimento? Interprete o modelo.
Analise os residuos do modelo no item e comente as suas descobertas.
Passo 1
Bom galera, vamos usar o Minitab para estimar o efeito dos fatores, colocando os dados, nós teremos:
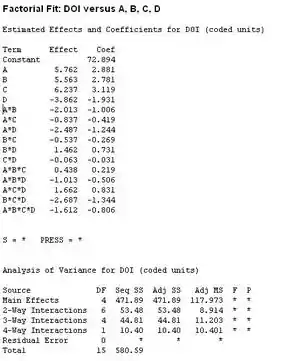
Passo 2
Belezinha, agora vamos plotar um gráfico de probabilidade normal dos efeitos, ainda pelo Minitab, fica assim:
Com esse gráfico nós podemos inferir que todos os fatores não são significantes. A partir desse gráfico, nós não podemos criar um modelo experimental.
Passo 3
Agora, vamos fazer nossa analise de variância, temos como resultado:
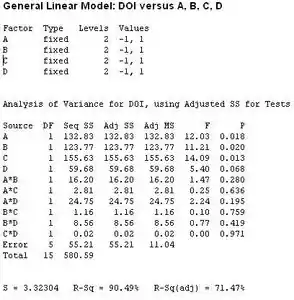
Pegamos na tabela de anasile de variância o valor do , e é menor do que . Portanto, os fatores , e são significantes.
Passo 4
Então, temos o modelo para descrever o processo:
Onde a intercessão é a média de todas as observações e é a metade do efeito estimado para , o efeito é o estimado para e é o efeito estimado para .
Passo 5
Por fim, vamos montar uma tabelinha com os valores previstos e os resíduos:
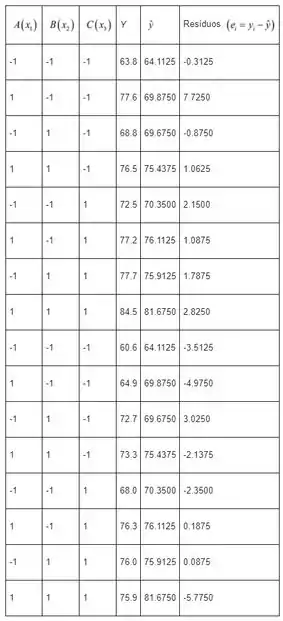
Plotando o gráfico de normalidade dos resíduos ficamos com:
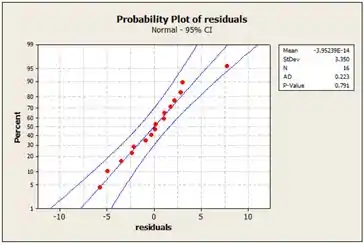
E vemos que os resíduos estão aproximadamente ao longo de um linha reta. Portanto, não há nenhum problema com a normalidade nos dados.
Resposta
; ; ; ; ; ; ; ; ; ; ; ; ; ;
Todos os fatores insignificantes, logo não tem nenhum modelo para prever respostas do experimento.
Os fatores , e são significantes.
A intercessão é a média de todas as observações e é a metade do efeito estimado para , o efeito é o estimado para e é o efeito estimado para .
Os resíduos estão aproximadamente ao longo de um linha reta. Portanto, não há nenhum problema com a normalidade nos dados.