Reconsidere os dados da espessura do oxido no Exercicio 7-23c suponha que seja razoavel supor que a espessura do oxido seja normalmente distribuida.
- Calcule as estimativas de maxima verossimilhanca de p e de o.
- Faca um grafico da funcio verossimilhanca na vizinhanca de ji eo e das estimativas de maxima verossimilhanca e comente a sua forma.
- Suponha quc o tamanho da amostra foi maior( ).porem as estimativas de maxima verossimilhanca foram numericamente iguais aos valores obtidos no item(a).Faca um grafico da funcao verossimilhanca para ,compare-o aquele do item(b)e comente sobre o efeito do maior tamanho de amostra.
Passo 1
Letra a:
A estimativa da média é
em nosso caso, , portanto
onde somamos todos os dados.
A estimativa da variância é
que é parcial.
Vamos calcular o estimador parcial da variância como
A estimativa do desvio padrão é a raiz quadrada da variância, portanto
Passo 2
Letra b:
A função de verossimilhança para uma amostra aleatória de tamanho n é:
onde são as datas que temos.
Os gráficos são:
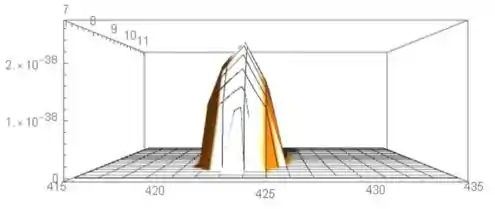
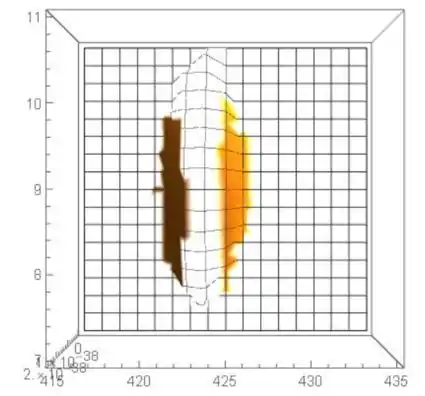
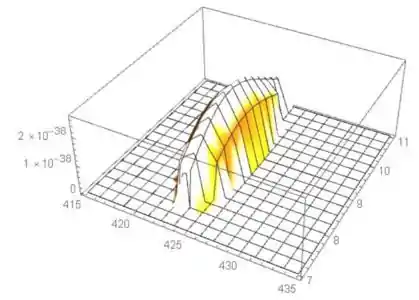
A função se parece com uma crista e a curvatura não é grande. O valor máximo está em 8.89 (desvio padrão) e 423.33 (a média).
Passo 3
Letra c:
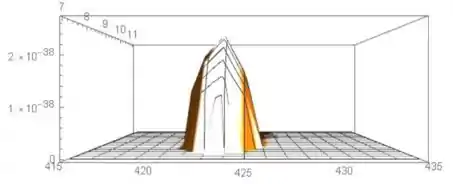
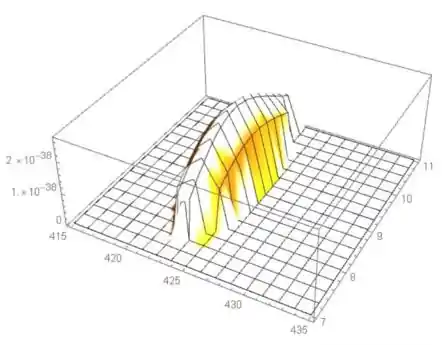
O gráfico não muda muito. Parece que é mais fácil determinar o valor máximo para o desvio padrão à medida à medida que aumenta.
Basicamente, apenas a curvatura será maior (não significativamente).
Resposta
- Ver resolução
- Ver resolução