Um artigo na revista Solid State Techonology (Vol. 29, 1984, pp. 281-284) descreve o uso de planejamentos fatoriais em fotolitografia, uma importante etapa no processo de fabricação de circuitos integrados. As variáveis nesse experimento (todas com dois níveis) são temperatura de pré-cozimento (), tempo de pré-cozimento () e energia de exposição (); a variável de resposta é largura da linha delta, a diferença entre a linha na máscara e a linha impressa no dispositivo. Os dados são:

; ; ; ; ; ; e .

Estime os efeitos do fatores.

Use o gráfico de probabilidade normal das estimativas dos efeitos para identificar fatores que podem ser importantes.

Que modelo você recomendaria para prever a resposta largura da linha delta baseado nos resultados desse experimento?

Analise os resíduos desse experimento e comente a adequação do modelo.

Beleza, A estimativa dos efeitos dos fatores fica:

Show de bola, agora no Minitab, construímos um gráfico de probabilidade normal dos efeitos. Fica assim:

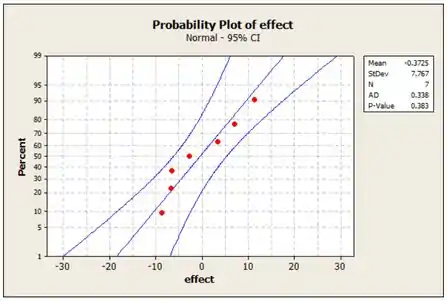
Pelo gráfico vemos que não temo nenhum fator não significante, porque todos os pontos estão próximos da linha reta.

Por fim, realizamos a analise de variância pelo Minitab, o resultado é:

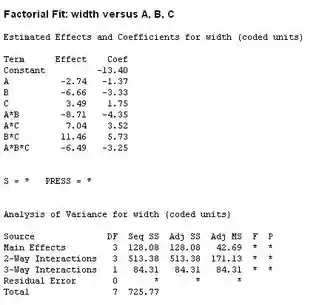
Com essa análise e o gráfico normal feito antes, todos os fatores insignificantes. Portanto, não tem nenhum modelo para prever a resposta da largura da linha delta.

Não existe nenhum gráfico de resíduos nesse experimento, pois o erro quadrado médio e o grau de liberdade do erro são .