Enunciado
Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 6.Exercícios - Ex. 25
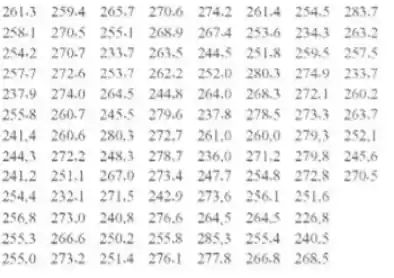
Associação norte-americana de golfe testa bolsas de golfe para assegurar que elas obedeçam as regras de golfe. Bolas são testados em relação a peso, diâmetro, redondeza e distância global. O texto de distância global é conduzido batendo nas bolas com um taco balançando por um dispositivo mecânico, apelidado de Iron Byron por causa do lendário Byron Nelson, cujo balanço emulado pelo dispositivo. A seguir, apresentam-se sem distâncias (em jardas) encontradas por uma marca particular de bolsa de golfe um teste distância global. Construa um diagrama de Ramos e folhas para esses estados e comente sobre importante característica que você note. Calcule a média, desvio padrão e a mediana da mostra. Qual é o 90º per sentiu das distâncias?
Passo 1
Arredonde todos os valores de dados para o número inteiro mais próximo.
261, 259, 266, 271, 274, 261, 255, 284, 258, 271, 255, 269, 267, 254, 234, 263, 254, 271, 234, 264, 245, 252, 260, 258, 258, 273, 254, 262, 252, 280, 275, 234, 238, 274, 265, 245, 264, 268, 272, 260, 256, 261, 246, 280, 238, 279, 273, 264, 241.261, 280, 273, 261, 260, 279, 252, 244, 272, 248, 279, 236, 271, 280, 246, 241, 251, 267, 273, 248, 255, 273, 271, 254, 232, 272, 243, 274, 256, 252, 257, 273, 241, 277, 265, 265, 227, 225, 267, 250, 256, 285, 255, 241, 255, 273, 251, 276, 278, 267, 269
Coloque os dígitos das dezenas à esquerda da linha vertical e os dígitos dos 1s de cada valor de dados à direita da linha vertical.
A distribuição parece estar inclinada para a esquerda, porque a maioria dos dados ficam perto da parte inferior do diagrama de ramo e folha.
Passo 2
Classifique os valores dos dados:
225,3, 226,8. 232,1, 233,7. 233,7, 234,3, 236, 237,8. 237,9, 240,5, 240,8, 241,2, 241,4, 242,9. 244,3, 244,5, 244,8, 245,5, 245,6, 247,7, 248,3, 250,2, 251,1, 251,4, 251,6, 251,8, 252, 252,1, 253,6. 253,7, 254,2, 254,4. 254,5, 254,8, 255, 255,1, 255,4. 255,8, 255,8, 256,1, 256,8, 257,5. 257,7, 258,1, 259,4, 259,5, 260, 260,2, 260,6, 260,7, 261, 261,3, 261,4. 262,2, 263,2, 263,5. 263,7, 264, 264,5, 264,5, 264,5. 265,7, 266,6. 266,8, 267. 267,4, 268,3. 268,5, 268,9, 270,5, 270,5, 270,6, 270,7, 271,2, 271,5, 272,1, 272,2, 272,6, 272,7, 272,8, 273, 273,2, 273,3, 273,4, 273,6, 274, 274,2, 274,9, 276,1, 276,6, 277,8. 278,5, 278,7, 279,3, 279,6, 279,8, 280,3, 280,3, 283,7, 285,3
A média é a soma de todos os valores dividido pelo número de valores:
A variância é a soma dos desvios quadrados da média dividida por n - 1. O desvio padrão é a raiz quadrada da variância:
Como o número de pontuações é par, a mediana é a média dos dois valores médios do conjunto de dados classificado:
n é o número de valores no conjunto de dados.
O 90º percentil precisa ter 90% dos 100 valores de dados abaixo dele que é 90 valores de dados e, portanto, o percentil é a média do 90º e 91º valor de dados do conjunto de dados classificado:
Resposta
Média: 260.002
Desvio-padrão: 13.8497
Mediana: 260.85
90º percentil : 277.2