Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.5 - Ex. 57
Um boxplot modificado é um boxplot que utiliza símbolos para identificar outliers. A linha horizontal desse boxplot se estende no lado esquerdo, até o menor valor dos dados que não seja outlier e, à direita até o maior dos dados que não seja um outlier. Nos exercícios 57 e 58, (a) identifique qualquer outlier e (b) desenhe um boxplot modificado que represente o conjunto de dados. Use um asterisco (*) para identificar outliers.
Passo 1
Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!
A – Ordenando todos os valores do conjunto de dados, nós temos que
O resumo de cinco números consiste no mínimo, primeiro quartil, mediana, terceiro
quartil e máximo. O mínimo (menor valor de dados) é 2. A mediana (segundo quartil) é o valor médio do conjunto de dados classificado
O primeiro quartil é a mediana dos valores dos dados abaixo da mediana (ou a 25% da
os dados):
O terceiro quartil é a mediana dos valores dos dados acima da mediana (ou em 75% da
os dados):
O máximo (o maior valor de dados) é 24
Passo 2
O intervalo interquartil é a diferença do terceiro e primeiro quartil
Outliers são observações que são mais de 1,5 vezes o IQR acima do Q3 ou abaixo do primeiro quartil (Q1).
Notamos, então, que 2 e 24 são valores do tipo outlier, porque 2 é menor que 7 e 24 é
maior que 19.
Passo 3
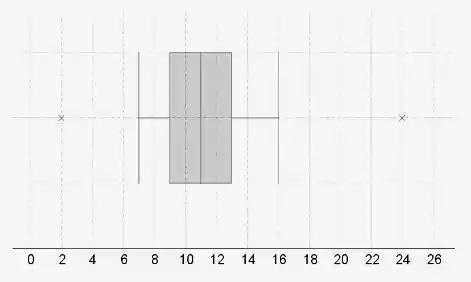
B - Os “bigodes” do boxplot estão no valor mínimo e máximo (não incluindo os outliers). A caixa começa no primeiro quartil, termina no terceiro quartil e tem uma linha vertical na mediana.
O primeiro quartil está em 25% da lista de dados ordenados, a mediana em 50% e o terceiro
quartil em 75%. "X" representa um outlier.
Resposta
A – 2 e 24 são outliers
B – Demonstrado no boxplot