Enunciado
Probabilidade e Estatística - Bussab - Estatística Básica- Ed: 9º - Capítulo 15.Problemas - Ex. 12
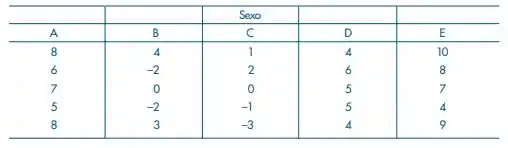
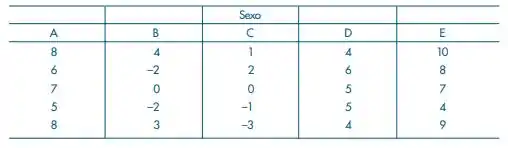
Os dados abaixo vêm de um experimento completamente aleatorizado, onde 5 processos de estocagem foram usados com um produto perecível por absorção de água. 25 exemplares desse produto foram divididos em cinco grupos de cinco elementos, e após uma semana mediu-se a quantidade de água absorvida. Os resultados codificados estão no quadro abaixo. Existem evidências de que os processos de estocagem produzem resultados diferentes?
Passo 1
Vamos lá.
Esses são os dados do nosso problema.
Queremos verificar se existem evidências de que os processos de estocagem produzem resultados diferentes. Para isso, vamos construir uma tabela ANOVA 😉.
Logo, temos um teste de comparação entre cinco médias. Como qualquer teste de hipótese, a primeira etapa é formular as hipóteses, para uma análise de variância, as hipóteses serão sempre assim:
Agora é partir para os cáculos.
Passo 2
Sabendo que
E calculando
Podemos montar nossa primeira tabelinha
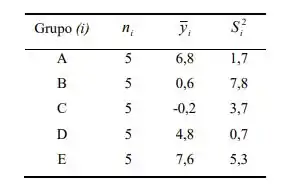
Olhando para as médias amostrais, vemos que elas têm valores diferentes, agora precisamos verificar se essa diferença é significativa, ou seja, se nós podemos dizer que baseados nessas diferenças que apareceram nas amostras, as populações são diferentes.
Vamos definir o nível de significância .
Passo 3
Agora, vamos calcular nossas informações que serão agrupadas numa única tabela, conhecida pelo nome de ANOVA, descrita na Tabela a seguir.
Basta aplicarmos as fórmulas que se encontram no Capítulo 10, calculando cada informação, temos
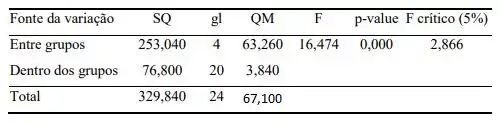
Para não perdemos tempo, na nossa tabela já constam os valores de F estatístico (16,474), p-valor (0,000) e F crítico (2,866) utilizando um , beleza? 😉
Passo 4
Para finalizarmos, vamos usar a estatística F. Analisando a tabela F: p = 5%, temos que F crítico é igual a 2,866, portanto como F estatístico é maior que F crítico. Rejeitamos , ou seja, os processos de estocagem não produzem todos o mesmo resultado.
Passo 5
Estamos quase acabando, beleza?
Na seção 15.4 é falado sobre “intervalos de Bonferroni”. Para prosseguir com o nosso problema, é recomendando que vocês leiam essa seção, é uma leitura bem rápida, ok?
Porém, nem tudo são flores, né? Caso, alguém não tenha entendido a leitura, eu fiz um pequeno resumo para vocês direto ao ponto, de o porquê usar o teste de Bonferroni 😉.
“Quando rejeitamos , verifica-se que é provável haver uma diferença entre as médias em estudo, pode-se buscar saber quais dentre as médias apresentam diferenças significativas. A partir disso, os procedimentos serão conduzidos de múltiplas comparações de médias, onde o teste de Bonferroni, na maior parte dos "design experiments", é muito útil.”
Agora, é partir para os cálculos mais uma vez.
Passo 6
Agrupando os dados numa única tabela, temos
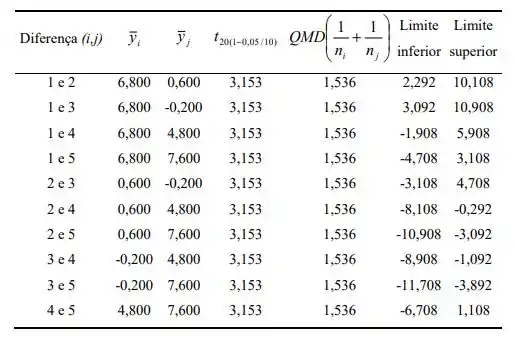
Conclusão:
Resposta
Sim, . Bonferroni indica