A Dra. Kelly Roberts é diretora de uma escola de medicina e tem a seu cargo o planejamento de cursos para calouros. O presidente do conselho da escola está encorajando-a a aumentar a ênfase em pediatria, mas a Dra. Roberts alega que menos de 10% dos estudantes de medicina dos EUA preferem pediatria, baseando essa alegação em dados amostrais que indicam que 64 dentre 1068 estudantes de medicina, selecionados aleatoriamente, escolheram a pediatria (com base em dados da Association of American Medical Colleges). Ao nível de 0,01 de significância, há evidência suficiente para apoiar o argumento da Dra. Roberts?

Agora vamos definir a estatística relevante para esse problema.

Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.

Então a nossa distribuição é aproximada pela distribuição normal.

Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.

Como o nosso teste é unilateral esquerdo, temos na cauda esquerda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.

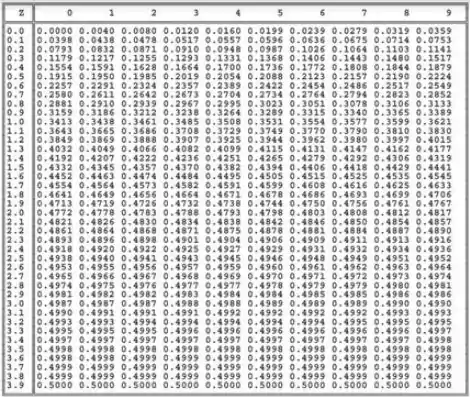
Pela tabela, obtemos o valor crítico:

Vamos dar uma olhada no gráfico abaixo:

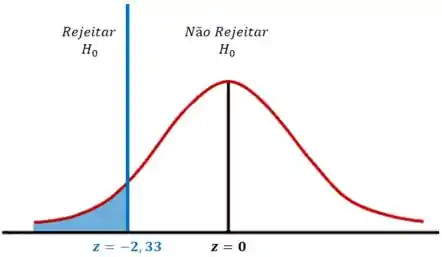
Como está dentro da região crítica, rejeitamos a hipótese nula .

Nesse exercício não conseguimos calcular o valor P, porque não é encontrado na tabela, mas como esse valor de é negativo e bem alto, e o nosso teste é unilateral esquerdo, podemos supor que o valor P vai ser muito pequeno e menor que , logo, rejeitamos .