A Federal Aviation Administration está disposta a subvencionar uma pesquisa sobre desorientação espacial dos pilotos, se houver evidencia amostral suficiente (no nível de 0,01 de significância) para concluir que, entre os acidentes com aeronaves que envolvem essa desorientação, mais de três quartos são casos fatais. Um estudo de 500 acidentes de avião envolvendo desorientação espacial do piloto revelou que 91% desses acidentes resultaram em fatalidades (dados do Departament of Transportation - EUA). Com base nesses resultados amostrais, a subvenção será aprovada?

Agora vamos definir a estatística relevante para esse problema.

Outra parada: vamos ver se podemos aproximar a nossa distribuição pela distribuição normal.

Então a nossa distribuição é aproximada pela distribuição normal.

Como vamos trabalhar com uma distribuição normal, o passo agora é calcular a estatística de teste.

Como o nosso teste é unilateral direito, temos na cauda direita, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.

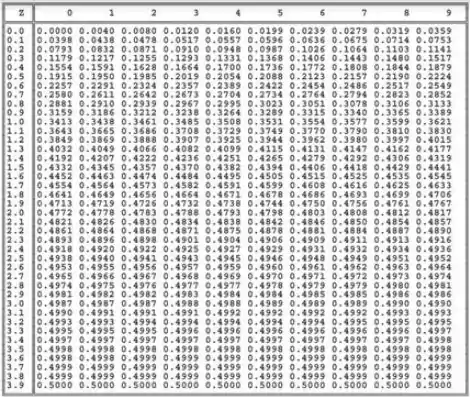
Pela tabela, obtemos o valor crítico:

Vamos dar uma olhada no gráfico abaixo:

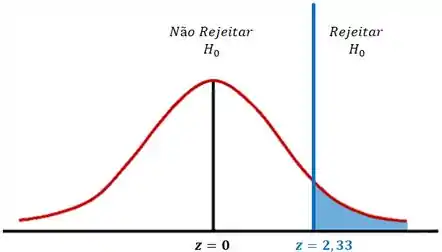
Como está dentro da região crítica, rejeitamos a hipótese nula .

Nesse exercício não conseguimos calcular o valor P, porque não é encontrado na tabela, mas como esse valor de é positivo e bem alto, e o nosso teste é unilateral direito, podemos supor que o valor P vai ser muito pequeno e menor que , logo, rejeitamos .