Enunciado
Probabilidade e Estatística - Estatística Aplicada Farber e Larson- Ed: 6º - Capítulo 2.3 - Ex. 58
Exportações dos EUA. A tabela a seguir mostra as exportações dos Estados Unidos (em bilhões de dólares) para 19 países em um ano recente. (Fonte: U. S. Department of Commerce).
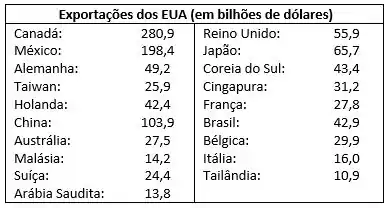
(a) Calcule a média e a mediana das exportações.
(b) Calcule a média e a mediana sem as exportações para o Canadá. Qual medida de tendência central, a média ou a mediana, foi mais afetada pela eliminação dos dados do Canadá?
(c) As exportações americanas para a Índia foram de US$ 21,5 bilhões. Encontre a média e a mediana acrescentando as exportações para a Índia aos dados originais. Qual medida de tendência central foi mais afetada pela inclusão dos dados da Índia?
Passo 1
Cálculo do item (a):
Para o cálculo da média, utilizamos a seguinte equação:
Onde:
valores dados
número de elementos do conjunto de dados
Temos que:
e , então:
Para o cálculo da mediana, iremos construir o ROL em ordem crescente:
Como temos , valor ímpar, então a mediana () é o valor central do conjunto numérico:
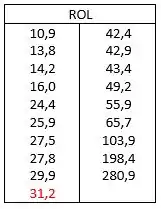
* valor central
Passo 2
Cálculo do item (b):
Eliminar os dados do Canadá da tabela:
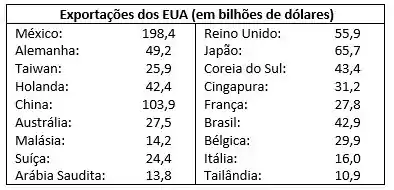
Calcular a média, como descrito anteriormente:
e , então:
Para o cálculo da mediana iremos construir o ROL em ordem crescente, porém, neste caso temos , número par, portanto para obter o valor da mediana () devemos fazer uma média aritmética dos dois números centrais.
* valores centrais
Passo 3
Cálculo do item (c):
Acrescentar os dados da Índia na tabela:
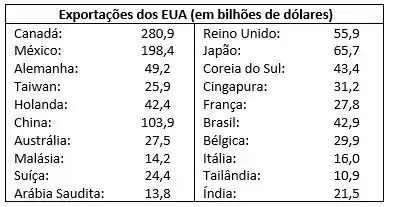
Calcular a média, como descrito anteriormente:
e , então:
Para o cálculo da mediana iremos construir o ROL em ordem crescente, porém, neste caso temos , número par, portanto para obter o valor da mediana () devemos fazer uma média aritmética dos dois números centrais.
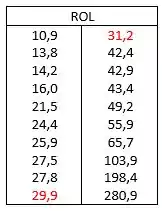
* valores centrais
Resposta
(a) e .
(b) e . A medida de tendência central mais afetada pela eliminação dos dados do Canadá foi a média.
(c) e . A medida de tendência central mais afetada pela inclusão dos dados da Índia foi a média.