Enunciado
Probabilidade e Estatística - Triola - Introdução à Estatística- Ed: 7º - Capítulo 7.6 - Ex. 16b
Para grandes números de graus de liberdade, podemos aproximar valores críticos de como segue:
Aqui, é o número de graus de liberdade e é o valor crítico, encontrado na Tabela A-2. Por exemplo, se queremos aproximar os dois valores críticos de em um teste de hipótese bilateral, com e , tomamos com , seguindo de e .
b. Com esta aproximação, estime os valores críticos de em um teste bilateral com e .
Passo 1
Fala ae, pessoal! Bora fazer esse exercício!
Como o enunciado nos diz: temos um teste bilateral. Como o nosso teste é bilateral, temos em cada cauda, então procuramos uma área de na tabela ai de baixo. O valor mais próximo disso também serve.
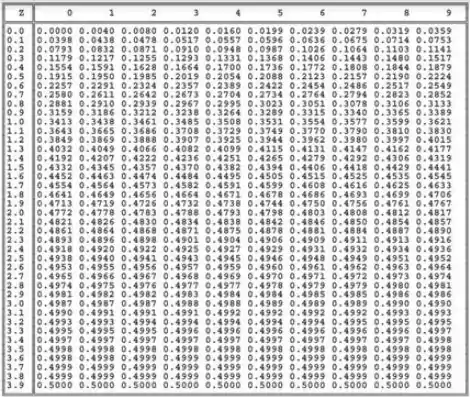
Pela tabela, obtemos o valor crítico:
Passo 2
Como , temos:
Assim podemos calcular os dois valores críticos.
Usando para encontrar o valor crítico da esquerda, temos:
Usando para encontrar o valor crítico da direita, temos:
Resposta
Utilizando esta aproximação, os valores críticos estimados são: 116,643 e 184,199.