Quando os home runs são muitos em um jogo de beisebol, há suspeitas de que bolas novas estejam “viciadas” para que alcancem uma distância maior. Testes feitos em bolas velhas mostraram que, quando liberadas de uma altura de 24 ft sobre uma superfície de concreto, elas replicam uma média de 92,83 in. Em um teste com uma amostra de 40 bolas novas, as alturas dos repiques acusaram média de 92,67 in. e desvio-padrão de 1,79 in. (com base em dados da Brookhaven National Laboratory e de USA Today). Com um nível de 0,05 de significância, teste a afirmação de que as novas bolas apresentam repiques de alturas diferentes de 92,84 in. Essas bolas são “viciadas”? Identifique também o valor P. Suponha que todas as amostras tenham sido extraídas aleatoriamente.
Passo 1
Tudo certo, pessoal? Bora continuar a fazer mais uns exercícios de teste de hipótese! São vários passos, mas não precisa ter medo! É só repetir o processo que estávamos fazendo! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
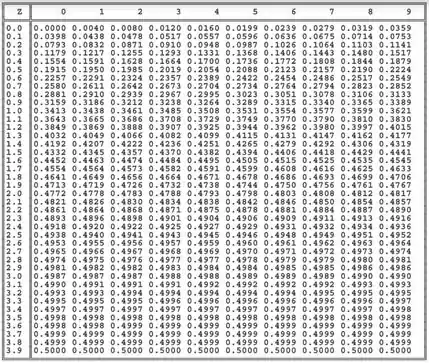
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será bilateral porque vamos testar a hipótese ):
Passo 2
Beleza! Agora temos que encontrar o Z a partir da fórmula de antes:
Em seguida, chegamos ao valor P () correspondente ao Z encontrado na tabela. Como o valor de Z é negativo em um teste bilateral, temos que olhar para a porção esquerda do gráfico, já que buscamos a seguinte situação:
Procuramos de novo os primeiros algarismos entre as linhas e o último entre as colunas. Assim, percebemos que, ao procurar por Z=-0,60, encontramos um valor de . Assim, chegamos a .
Passo 3
Passo final! Para acabar o teste de hipóteses, é só compararmos o valor de e . Nesse caso, e . Como o valor P () é maior que , concluímos que não podemos rejeitar . Assim, a afirmação é inadequada.
E pronto! Acabamos! Simples, né?
Resposta
e .
não é rejeitada. A afirmação é inadequada, logo as bolas não estão “viciadas”.