Em um estudo de hábitos de consumidores, pesquisadores elaboraram um questionário para identificar os compradores compulsivos. Para uma amostra de consumidores que se declararam compradores compulsivos, os resultados dos questionários acusaram média de 0,83 e desvio-padrão de 0,24 (com base em dados de “A Clinical Screener for Compulsive Buying”, por Faber e Guinn, Journal of Consumer Research, Vol. 19). Suponha uma amostra de 32 indivíduos selecionados aleatoriamente. No nível de 0,01 de significância, teste a afirmação de que a população dos que se identificam como compradores compulsivos tem média superior a 0,21, a média geral da população. O questionário parece ser eficiente para identificar os compradores compulsivos? Identifique também o valor P. Suponha que todas as amostras tenham sido extraídas aleatoriamente.
Passo 1
Tudo certo, pessoal? Bora continuar a fazer mais uns exercícios de teste de hipótese! São vários passos, mas não precisa ter medo! É só repetir o processo que estávamos fazendo! Vamos ter que usar uma tabela de distribuição normal de novo! Trouxe aqui uma imagem dela pra vocês!
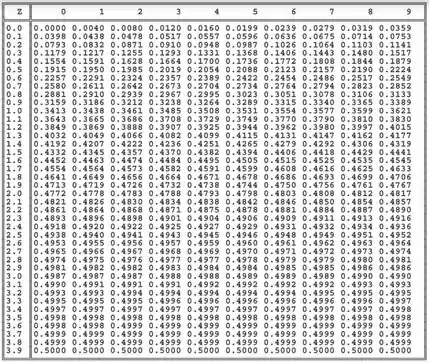
Também vamos precisar usar a fórmula do Z para um Teste de Hipóteses para média (com conhecido ou ):
Primeiro, vamos determinar os valores iniciais do problema, montando e (já sabemos que o teste será unilateral direito porque vamos testar a hipótese ):
Passo 2
Beleza! Agora temos que encontrar o Z a partir da fórmula de antes:
Em seguida, chegamos ao valor P () correspondente ao Z encontrado na tabela, já que buscamos a seguinte situação:
Dessa vez, como o valor de z é muito grande (14,61), o que pode também ser um erro por parte do problema, assumimos que 0,500 é o valor que procuramos. Assim, chegamos a .
Passo 3
Estamos no final! Agora, para acabar o teste de hipóteses, é só compararmos o valor de e . Nesse caso, e . Como o valor P () é menor que , concluímos que devemos rejeitar . Assim, a afirmação está correta.
E pronto! Acabamos! Simples, né?
Resposta
e .
é rejeitada. A afirmação está correta.