Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Probabilidade e Estatística - Montgomery - Estatística Aplicada e Probabilidade para Engenheiros- Ed: 4º - Capítulo 5.Exercícios - Ex. 1

Mostre que a seguinte função satisfaz as propriedades de uma função de probabilidade conjunta.

Determine o seguinte:

  1. P ( X < 2.5 ,   Y < 3 )
  2. P(X
  3. P ( Y < 3 )
  4. P ( X . 1.8 ,   Y > 4.7 )
  5. E ( X ) ,   E ( Y ) ,   V ( X )   e   V ( Y )
  6. a distribuição de probabilidade marginais da variável aleatória X.
  7. A distribuição de probabilidades condicionais de Y, dado que X = 1.5.
  8. A distribuição de probabilidades condicionais de X, dado que Y= 2.
  9. E ( Y | X = 15 )
  10. X e Y são independentes?

Passo 1

Uma função de massa de probabilidade conjunta válida deve satisfazer:

∑ x ∑ y f x y ( x , y ) = 1

Se X e Y forem variáveis ​​aleatórias discretas.

∑ x ∑ y f x y ( x , y ) = 1 4 + 1 8 + 1 4 + 1 4 + 1 8 = 1

Passo 2

Letra a:

Vamos encontrar a probabilidade de que X

P ( X < 2.5 ,   Y < 3 ) = P ( X = 1.5 ,   Y = 2 ) + P ( X = 1 ,   Y = 1 )

= 1 8 + 1 4

= 3 8

Passo 3

Letra b:

Vamos determinar a probabilidade de que X

P ( X < 2.5 ) = P ( X = 1.5 ,   Y = 3 ) + P ( X = 1.5 ,   Y = 2 ) + P ( X = 1 ,   Y = 1 )

= 1 4 + 1 8 + 1 4

= 5 8

Passo 4

Letra c:

Vamos encontrar a probabilidade de que Y

P ( Y < 3 ) = P ( X = 1.5 ,   Y = 2 ) + P ( X = 1 ,   Y = 1 )

= 1 8 + 1 4

= 3 8

Passo 5

Letra d:

Vamos calcular a probabilidade de que X > 1.8 e Y > 4.7 :

P ( X > 1.8 ,   Y > 4.7 ) = P ( X = 3 ,   Y = 5 )

= 1 8

Passo 6

Letra e:

Vamos encontrar E ( X ) ,   E ( Y ) ,   V ( X )   e V ( Y )

Vamos encontrar a média de X.

Primeiro, temos que encontrar a distribuição de probabilidade marginal de X:

P ( X = 1 ) = P ( X = 1 ,   Y = 1 ) = 1 4

P ( X = 1.5 ) = P ( X = 1.5 ,   Y = 2 ) + P ( X = 1.5 ,   Y = 3 )

= 1 8 + 1 4 = 3 8

P ( X = 2.5 ) = P ( X = 2.5 ,   Y = 4 ) = 1 4

P ( X = 3 ) = P ( X = 3 ,   Y = 5 ) = 1 8

A média de X será:

E ( X ) = ∑ x x P ( X = x )

= 1 × 1 4 + 1.5 × 3 8 + 2.5 × 1 4 + 3 × 1 8

= 1.8125

Vamos encontrar a variância de X:

V ( X ) = ∑ x x 2 P ( X = x ) - ( E ( X ) ) 2

= 1 2 × 1 4 + 1 . 5 2 × 1 4 + 3 2 × 1 8 - 1.812 5 2

= 0.4961

Vamos encontrar a variância de Y:

V ( Y ) = ∑   y y 2 P ( Y = y ) - ( E ( Y ) ) 2

1 2 × 1 4 + 2 2 × 1 8 + 3 2 × 1 4 + 4 2 × 1 4 + 5 2 × 1 8 - 2.87 5 2

= 1.8594

Vamos encontrar a média de Y:

Primeiro, temos que encontrar a distribuição de probabilidade marginal de Y:

P ( Y = 1 ) = P ( X = 1 ,   Y = 1 ) = 1 4

P ( Y = 2 ) = P ( X = 1.5 ,   Y = 2 ) = 1 8

P ( Y = 3 ) = P ( X = 2.5 ,   Y = 4 ) = 1 4

P ( Y = 4 ) = P ( X = 2.5 ,   Y = 4 ) = 1 4

P ( Y = 5 ) = P ( X = 3 ,   Y = 5 ) = 1 8

A média de Y é:

E ( Y ) = ∑ y y P ( Y = y )

= 1 × 1 4 + 2 × 1 8 + 3 × 1 4 + 4 × 1 4 + 5 × 1 8

= 2.875

Passo 7

Letra f:

A distribuição de probabilidade marginal de X é

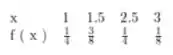
Passo 8

Letra g:

Vamos calcular a distribuição de probabilidade condicional de Y, dado que X = 1.5

f ( 2 ) = f y | 1.5 ( 2 ) = f x y ( 1.5,2 ) f x ( 1.5 ) = 1 8 3 8 = 1 3

f ( 3 ) = f y | 1.5 ( 3 ) = f x y ( 1.5,3 ) f x ( 1.5 ) = 1 4 3 8 = 2 3

Passo 9

Letra h:

Vamos encontrar a distribuição de probabilidade condicional de X dado que Y = 2:

f ( 1.5 ) = f x | 2 ( 1.5 ) = f x y ( 1.5,2 ) f y ( 2 ) = 1 8 1 8 = 1

Passo 10

Letra i:

Da parte da letra g:

P ( Y = 2 | X = 1 . 5 ) = 1 3

P ( Y = 3 | X = 1.5 ) = 2 3

Vamos encontrar a média condicional de Y dado que X = 1.5:

E ( Y | X = 1.5 ) = ∑ y y f Y | X = 1.5 ( y ) = 2 × 1 3 + 3 × 2 3 = 8 3

Passo 11

Letra j:

Vamos descobrir se as variáveis ​​aleatórias X e Y são independentes:

f x y ( x , y ) = P ( X = 1.5 ,   Y = 2 ) = 1 8

f x ( x ) f y ( y ) = P ( X = 1 . 5 ) P ( Y = 2 ) = 3 8 × 1 8 = 3 64

1 8 ≠ 3 64

Portanto, as variáveis ​​aleatórias X e Y não são independentes.

Resposta

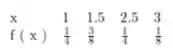
  1. 3 8
  2. 5 8
  3. 3 8
  4. 1 8
  5. E ( X ) = 1.8152 ,   E ( Y ) = 2.875 ,   V ( X ) = 0.4961 ,   V ( Y ) = 1.8594
  7. f ( 2 ) = 1 3 ,   f ( 3 ) = 2 3
  8. 1
  9. 8 3
  10. Portanto, as variáveis ​​aleatórias X e Y não são independentes.
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma gravidez ectópica é duas vezes mais provável em mulheres fumantes do que em mulheres não fumantes. Se 32% das mulheres na idade reprodutiva são fumantes, que percentual de mulheres com gravidez ec
Um dado vermelho, um azul e um amarelo (todos com seis lados) são rolados. Estamos interessados na probabilidade de que o número que sair no dado azul seja menor do que aquele que sair no dado amarelo
A urna I contém 2 bolas brancas e 4 bolas vermelhas, enquanto a urna II contém 1 bola branca e 1 bola vermelha. Uma bola é aleatoriamente escolhida da urna I e colocada na urna II, e então uma bola é
Cinquenta e dois por cento dos estudantes de certa faculdade são mulheres. Cinco por cento dos estudantes desta faculdade estão se formando em ciência da computação. Dois por cento dos estudantes são
Considere duas caixas, uma contendo 1 bola de gude branca e 1 branca, e a outra contendo 2 bolas de gude brancas e 1 branca. Uma caixa é selecionada aleatoriamente e uma bola de gude é retirada de for