Exercícios de Probabilidade Conjunta de V.A. Bidimensionais Discretas - Lista de Exercícios Resolvida
Questão 1
Considere a distribuição conjunta de X e Y, parcialmente conhecida, dada na tabela abaixo.
a) Complete a tabela, considerando X e Y independentes.
b) Obtenha as distribuições condicionais de X, dado que Y=0, e de Y, dado que X=1.
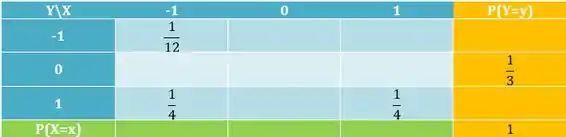
Questão 2
Numa urna têm-se cinco bolas marcadas com os seguintes números: -1, 0, 0, 0, 1. Retiram-se três bolas, simultaneamente: X indica a soma dos números extraídos e Y o maior valor da trinca. Calcule:
a) A função de probabilidade de (X,Y).
Ver solução completaQuestão 3
Uma urna contém 3 bolas brancas e 2 bolas vermelhas. Um experimento consiste em se extrair sequencialmente e sem reposição duas bolas e registrar suas cores. Seja a v.a. que representa o número de bolas brancas retiradas nas duas extrações e seja a v.a. que assume 1 se a primeira bola extraída é branca e 0 se a primeira bola extraída é vermelha.
- Obtenha a distribuição conjunta de e através de uma tabela e diga se e são independentes, justificando. Sugestão: Na montagem da tabela, comece determinando as distribuições marginais de e de . Em seguida, obtenha e . Finalmente complete a tabela, respeitando as propriedades de uma distribuição conjunta.
Questão 4
Lançam-se, simultaneamente, uma moeda e um dado.
a) Determine o espaço amostral correspondente a esse experimento.
b) Obtenha a tabela da distribuição conjunta, considerando X o número de caras no lançamento da moeda e Y o número da face do dado.
d) Calcule:
- P(X=2,Y=3)
Questão 5
Numa urna têm-se cinco tiras de papel, numeradas 1,3,5,5,7. Uma tira é sorteada e recolocada na urna, então uma segunda tira é sorteadas. Sejam o primeiro e o segundo números sorteados.
a) Determine a distribuição
b) Obtenha as distribuições marginais de
Ver solução completaQuestão 6
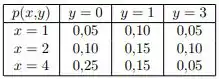
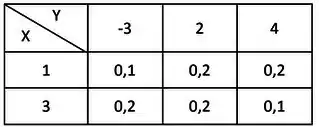
Foi feito o loteamento de uma área rural em terrenos retangulares. Para cada terreno, seu comprimento e sua largura, ambos em metros, podem ser iguais a , ou . Para simplificar, vamos trabalhar em decâmetros (simbolicamente, ), lembrando que . Assim, tanto o comprimento como a largura de um terreno sorteado ao acaso, podem ser iguais a 1, 2 ou 3. A tabela a seguir fornece (apenas parcialmente) a distribuição conjunta de e , variáveis aleatórias supostas independentes:
Considere as v.a.’s perímetro do terreno e área do terreno (em ).
Nessas condições, calcule:
(a) o valor de cada probabilidade, conjunta ou marginal, omitido na tabela acima.
(b) a probabilidade condicional de que a área seja igual a , dado que o perímetro é igual a .
(c) a média e a variância da área do terreno nesse loteamento.
Ver solução completaQuestão 7
Suponha e dois valores de probabilidade conhecidos. Assumindo duas v.a.’s discretas com distribuição conjunta para , e . Mostre como encontrar:
- O valor de , em função de e , para que seja uma distribuição conjunta. E escreva a função conjunta.
- A marginal de e de e indique qual o nome (modelo) destas distribuições.
- Podemos afirmar que e são independentes? Justifique sua resposta.
Questão 8
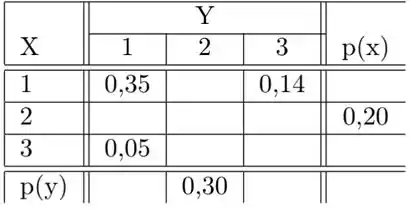
15) Um shopping de São Paulo possui um supermercado e uma farmácia. Sejam as variáveis aleatórias e que representam o número de vezes que um cliente assíduo desse shopping faz compras no supermercado e na farmácia durante um mês, respectivamente. A distribuição de probabilidade conjunta está na tabela abaixo. O valor médio do número de vezes que um cliente faz compra no supermercado dado que comprou vezes na farmácia vale:
A)
B)
C)
D)
E)
Ver solução completaQuestão 9
Quando os consumidores abastecem seus carros em determinado posto de gasolina situado beira de uma estrada, eles sempre aproveitam para fazer também uma refeição no restaurante self-service desse posto. Cada vez que isso acontece:
(1) O carro só é abastecido com um tipo de combustível, a saber, só com gasolina ou só com álcool.
(2) 70% dos carros usam gasolina e 30% usam álcool. Seja W ∼ Bernoulli(p), com p = 0,7, onde W = 1 corresponde a gasolina e W = 0 corresponde a álcool.
(3) A quantidade X de combustível em litros (de gasolina ou de álcool) colocada no tanque do veículo é Normal com média e desvio padrão
(4) O preço da gasolina é e o preço do álcool é .
(5) A quantidade Y de comida, em quilos, consumida em uma refeição no restaurante é Normal com média µY = 0,5 e desvio padrão σY = 0,2.
(6) O preço da comida no restaurante é γ = 30 reais/quilo.
(7) Há independência entre as variáveis aleatórias W, X e Y .
Então, T = [αW + β(1 − W)]X + γY é o montante dos gastos em reais, com combustível e com alimentação, durante uma parada nesse posto de um consumidor selecionado aleatoriamente. Calcule:
a)A distribuição da despesa total T, dado que o carro é abastecido com gasolina
(b) A distribuição da despesa total T, dado que o carro é abastecido com álcool.
(c) A média e o desvio padrão dessa despesa total T (sem separar pelo tipo de combustível).
(d) A probabilidade de que ele gaste ao todo no máximo 150 reais, ou seja, .
Sugestão: Use o Teorema da Probabilidade Total, condicionando em W.
Ver solução completaQuestão 10
Duas variáveis aleatórias, , apresentam a distribuição conjunta de probabilidade dada na tabela a seguir.
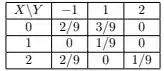
Calcule .
Ver solução completaQuestão 11
b) Seja variável aleatória discreta com a seguinte distribuição de probabilidade conjunta:
Pede-se:
Calcular e o Coeficiente de Correlação
Observação:
- Demonstrar a expressão da Covariância.
- Mostre os resultados considerando 4 casas decimais.
Ver solução completaQuestão 12
Suponha e dois valores de probabilidade conhecida. Assumindo duas v.a.’s discretas com distribuição conjunta , para e , mostre como encontrar:
- O valor de em função de e , para que seja uma distribuição conjunta. Apresente a função conjunta somente em função de e .
- A densidade condicional de dado
- Podemos afirmar que e são independentes? Justifique sua resposta.
Questão 13
Suponha e dois valores de probabilidade conhecidos. Assumindo duas v.a.’s discretas com distribuição conjunta para , e . Mostre como encontrar:
- O valor de , em função de e , para que seja uma distribuição conjunta. E escreva a função conjunta.
- A marginal de e de e indique qual o nome (modelo) destas distribuições.
- Podemos afirmar que e são independentes? Justifique sua resposta.
Questão 14
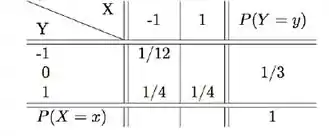
Considere a distribuição conjunta de e , parcialmente conhecida, dada pela tabela abaixo.
(a) Complete a tabela, considerando e independentes.
(b) Calcule as médias e variâncias de e .
(c) Calcule .
Questão 15
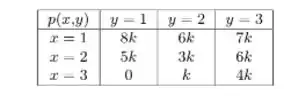
Para X e Y duas variáveis aleatórias discretas, que possuem distribuição conjunta de acordo com a tabela abaixo, quais são os valores de ?
Questão 16
10) A tabela abaixo mostra a distribuição de probabilidade conjunta de duas variáveis discretas . Não foram mostrados os valores de e mas sabe-se que as duas variáveis são independentes.
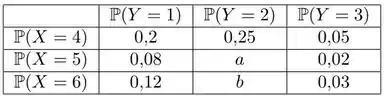
Determine .
a)
b)
c)
d)
e)
Ver solução completaQuestão 17
Todos os dias um técnico especializado em aparelhos de ar condicionado recebe chamados para atendimento domiciliar e, às vezes, ele leva consigo alguns auxiliares em todas as visitas do dia. Defina as variáveis aleatórias Y , número de atendimentos a fazer em um dia, e X, número de auxiliares que trabalham com ele naquele dia. A tabela a seguir apresenta a distribuição conjunta de X e Y .
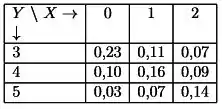
a) As variáveis X e Y são independentes? Justifique a resposta.
b) Calcule a probabilidade de X = k dado que Y = 5, para cada valor possível de X.
c) Calcule , ou seja, o número médio de auxiliares por atendimento.
Ver solução completa